2019年度北海道大学 後期 物理の問題を分析します。前期の問題分析は前回記事になります。
[kanren postid="1133"]１．問題構成
| 大問１ | 力学 | 動く4半円形の台上での円運動 | 《定番 優しめ》 |
| 大問２ | 電磁気 | 斜面上をすべる導体棒による電磁誘導 | 《定番 優しめ》 |
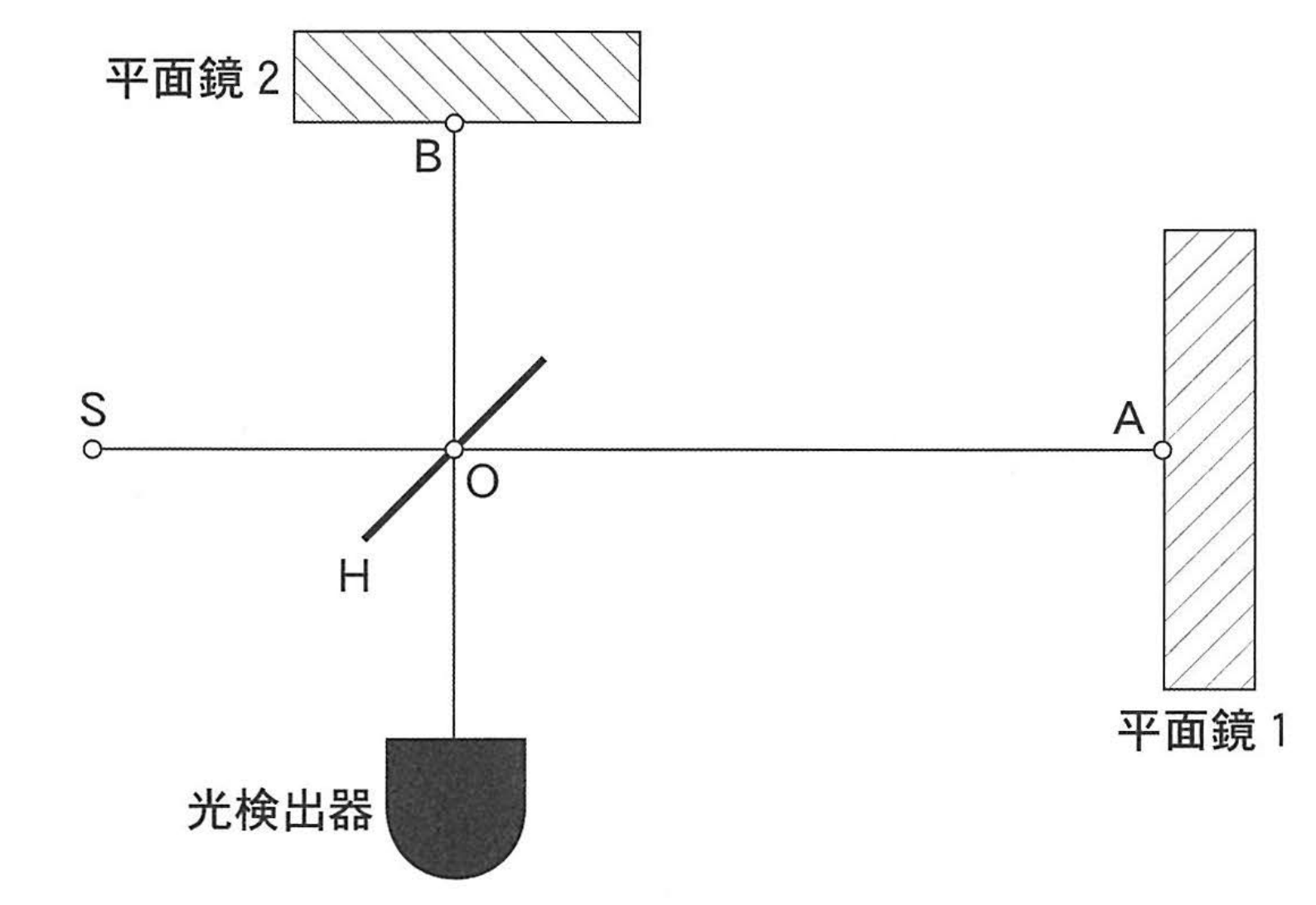
| 大問３ | 波動 | マイケルソン干渉計と屈折 | 《難しめ》 |
問題のダウンロードはこちらから（リンク切れとなりました）
２．かかった時間
かかった時間：８５分（試験時間は２科目で１５０分または１科目で７５分）
前期同様、時間内では解き終わりませんでした。
ただし、大問３に４０分、大問１、大問２合わせて４５分、という感じでしたので、大問３をスムーズにやれれば時間内に解き終わることは十分可能でした。計算力が年々落ちていってます………
北大志望の生徒は、手早く計算できるように練習しておくことが必要ですね。計算自体の難易度は高くありません。
３．筆者の正答率と各問題のポイント
| 大問１ | (14)で、m=Mを代入せず解答としてしまった（1問間違え） |
| 大問２ | 完答 |
| 大問３ | 完答？（最後の作図の採点基準が不明） |
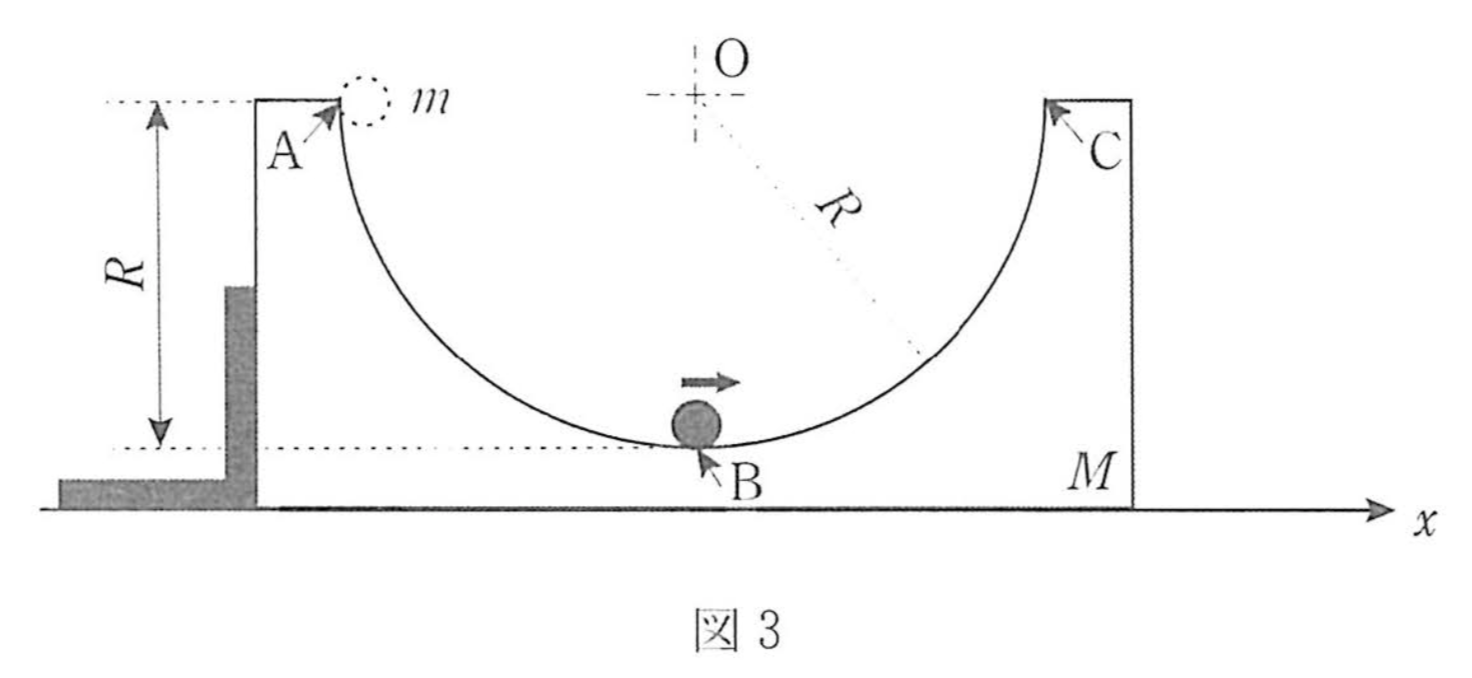
大問１について
前期の大問１とほぼ同じ。大学受験後半に放物運動の要素が追加されてます。
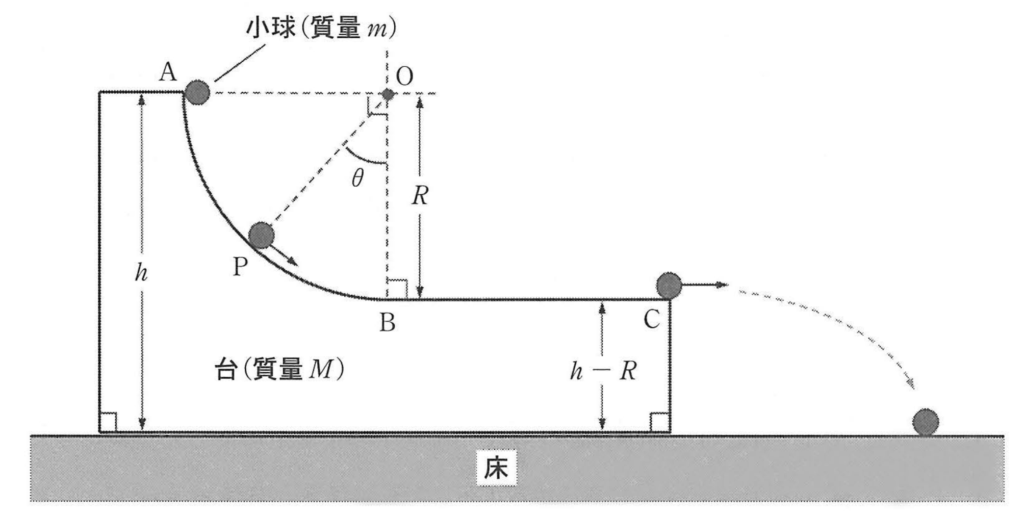
前半部分での誘導が丁寧ではなく、自分で文字を設定し、運動量保存、エネルギー保存の式を立てることが要求されます。
典型問題ではありますが、慣れが足りない生徒は、いつもよりも誘導が少ないせいで、戸惑った可能性があります。
また、最後の問題(13)(14)に関しては「２物体であること」「移動した距離」を聞かれていることから観測者を台上に立たせようとする生徒が多かったかもしれません。
しかし、与えられた距離Lが、２物体の位置の差なので観測者を特別なところにおく必要がなく、丁寧に作図をできれば立式は簡単に思いつけるはずです。
積極的に絵を書く習慣がない生徒は厳しかったかもしれません。
大問２について
最初から最後まで典型問題だったので、この大問は完答しておきたいです。
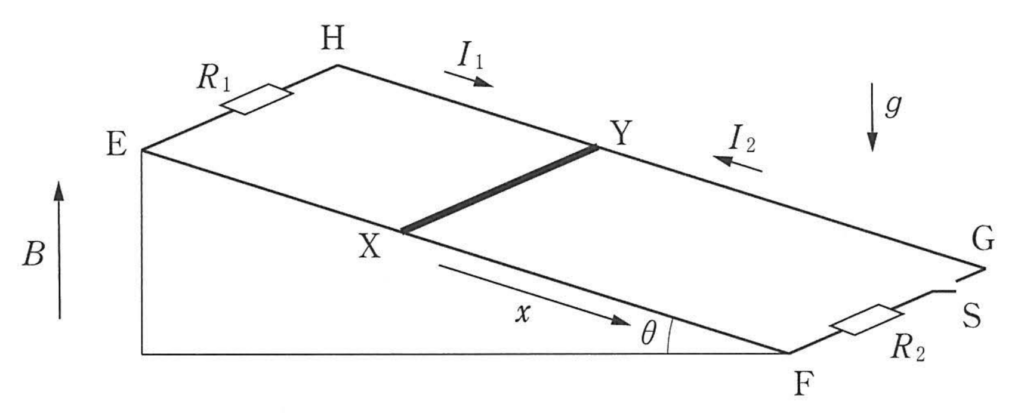ほらね！！図もいつも出てくるやつそのままです。
しかし、生徒（特に現役生）は電磁誘導でのエネルギー収支に関しては無頓着になりがちなので、後半で差がつく可能性はあったと思います。
電磁誘導を授業で扱う際、どんな問題でも、最後にエネルギー収支の問いかけを教員が投げかけるべきだと私は思います。
大問３について
この年の問題の核はここ、大問３です。
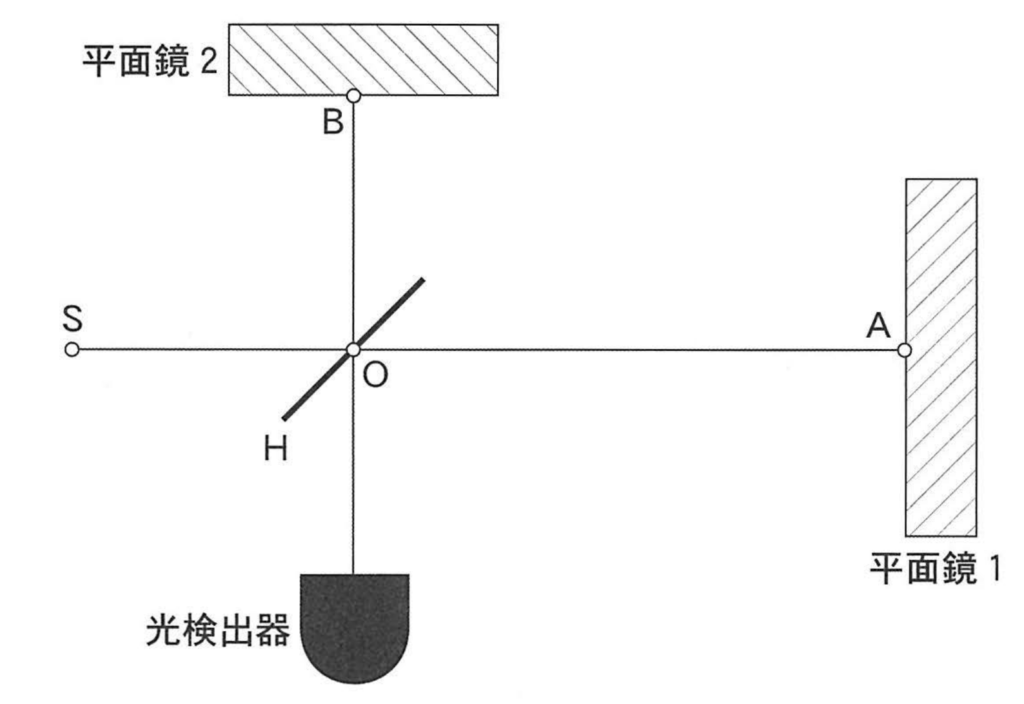
装置自体は普通のマイケルソン干渉計です。そしてマイケルソン干渉計のよくある問題は、平面鏡１や２を動かします。
しかしこの問題は、中央の鏡Oを動かします。
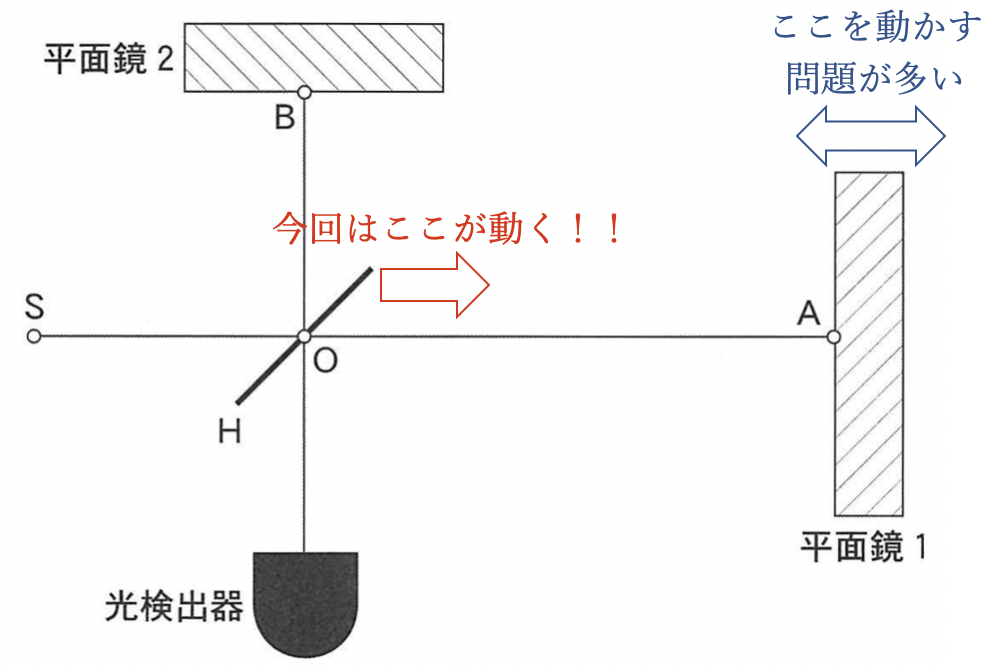
このとき経路差がどのように変化するかは、きちんと作図を行わないと想像しづらいです。作図を怠る生徒は戸惑う問題となったでしょう。
せっかくなので経路がどのように変化するか作図してみます。
【経路１について】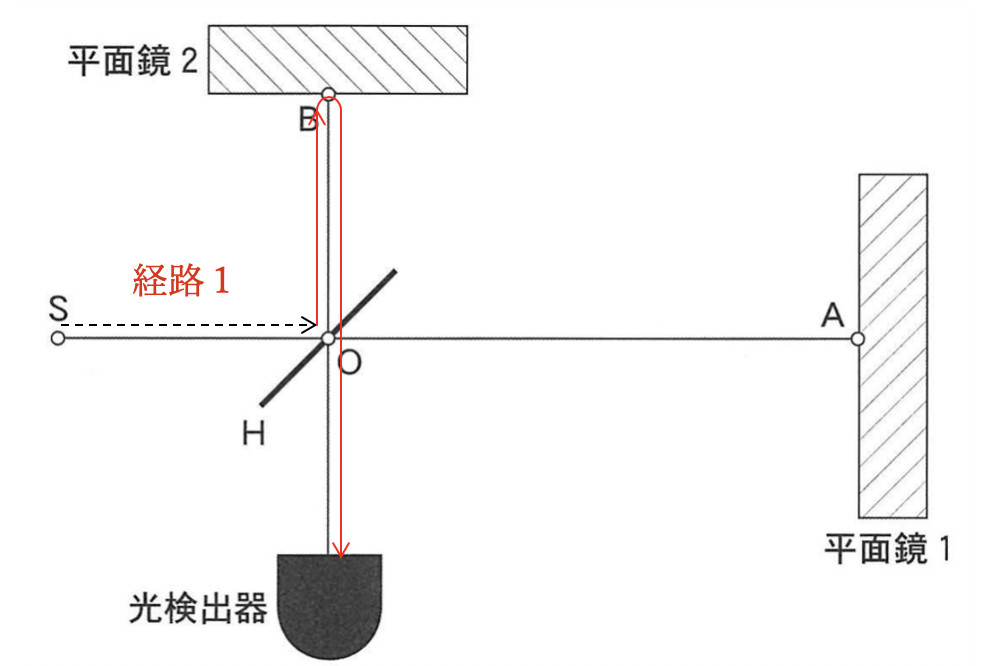
以上が経路１です。ここで、中央の鏡Oが動くと、
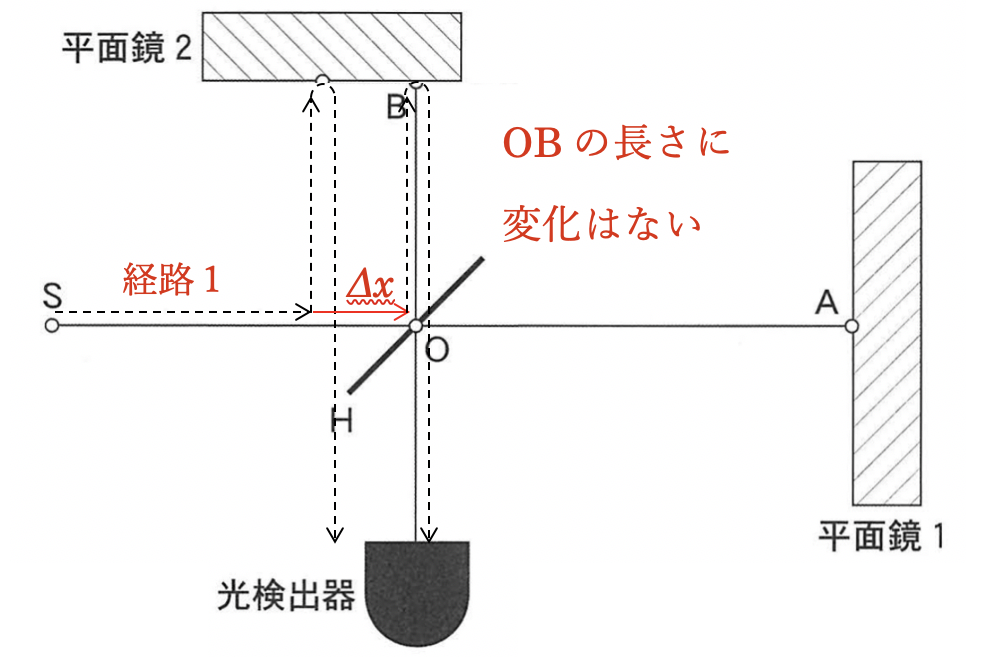
このように経路が変わります。このときOBの長さは変わっていないことがわかります。
【経路２について】
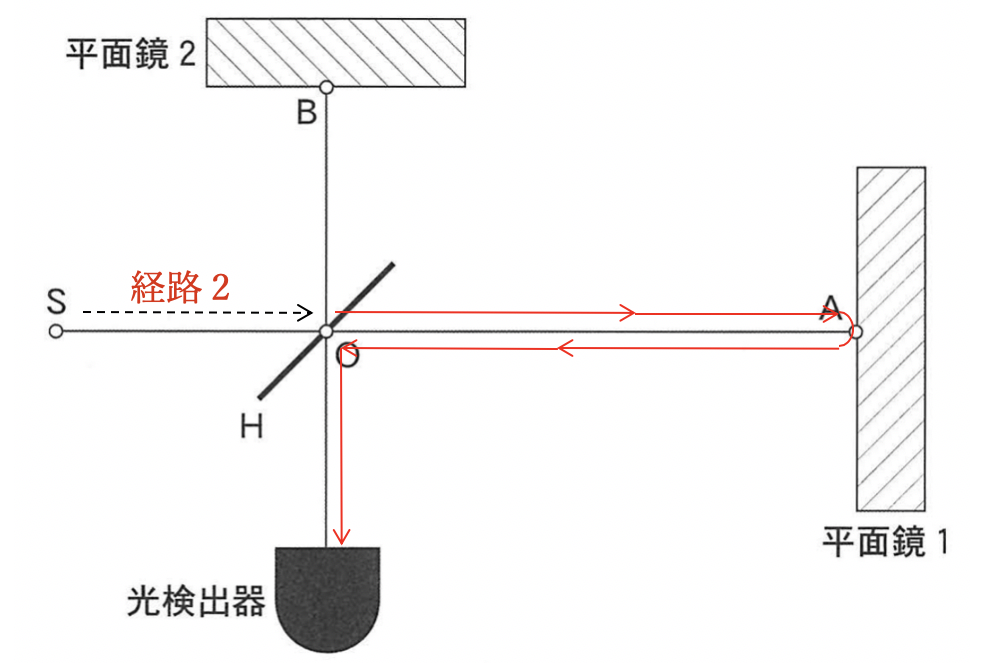
以上が経路２です。中央の鏡Oが動くと、
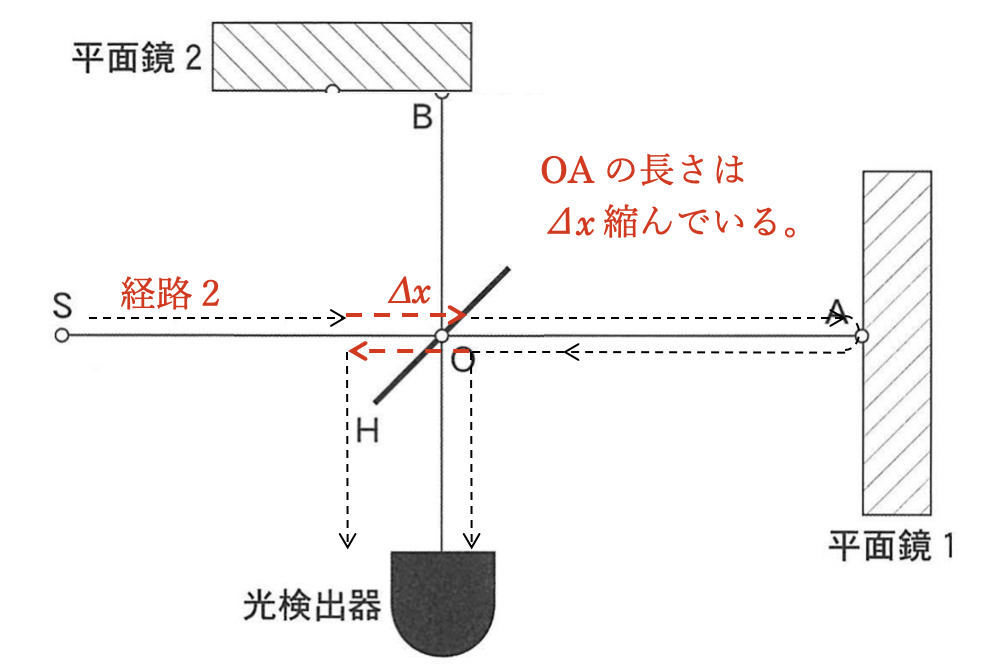
このように経路が変わります。赤点線の部分だけ、OAの長さが縮むといえます。
OB、OA以外の経路は、2つの経路で共通なので経路差には関わらないので、
（経路差）＝（２OAー２OB）＝２（OAーOB）
といえます。よって、OAがΔx縮んだとき、経路差は２Δx小さくなるといえます。
経路差が小さくなることがわかったら、あとは丁寧に干渉の式を立てて行くだけです。
生徒はこう間違えそう
ここで「経路１の方は、経路がΔx伸びていて、経路２の方は経路がΔx縮んでいるから、差し引き経路差が変わらないのでは？」という質問が出るかなとも思いました。図で説明します。
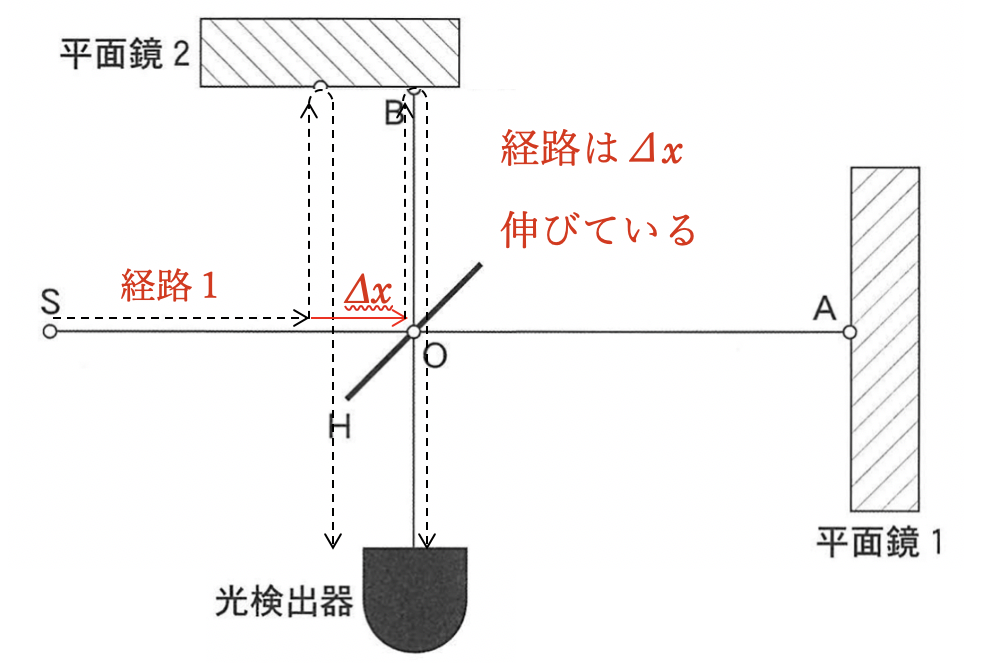
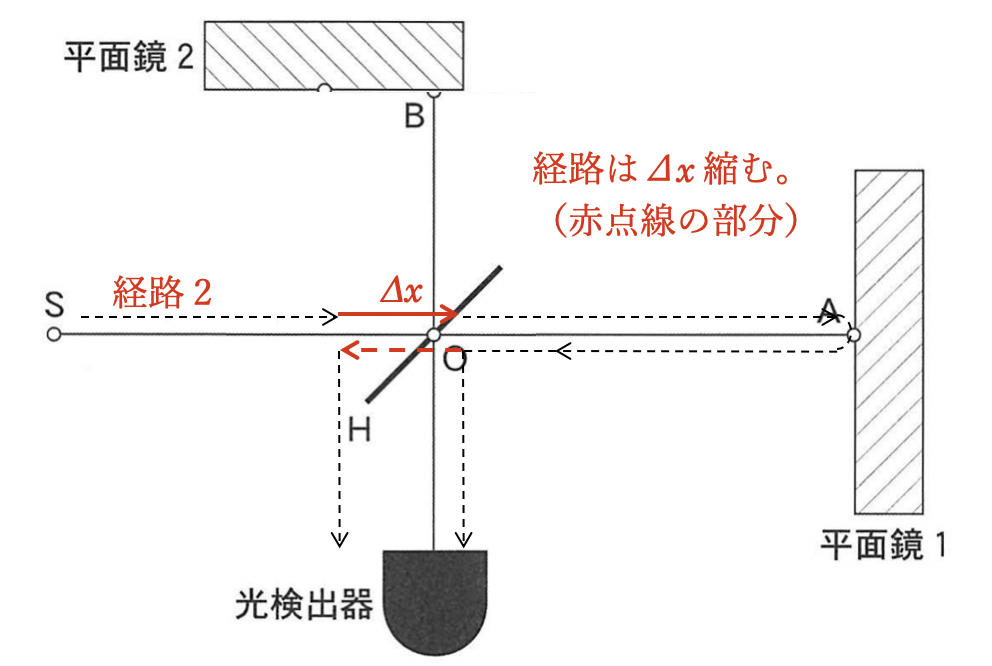
片方が伸びて、片方が縮んでいるのだから、経路の変化はプラマイ０なのでは？と考えてしまうパターンです。直感で考えてしまうとこうなる可能性があります。
これは経路差が
（経路差）＝（経路２の長さ）ー（経路１の長さ）
という計算で求めていると考えられれば納得すると思います。
経路２の長さがΔx小さくなり、経路１の長さがΔx大きくなれば、この式で求まる（経路差）は２Δx小さくなります。
長さの差が小さくなっているのです。
問題の誘導のように「経路の違う部分だけに着目する方法」と、このように「全体の経路の長さの差をとる方法」、両方の視点から経路差を考えることは様々な場面で役立つと思います。演習の際は両方扱うようにしたいですね。
４．北海道大学まとめ
後期に関しての合否の分かれ目はとにかく大問３でした。
大問３は
問１ 作図をきちんと行い、何がおきているか把握できたか
問２ 媒質をいれたとき、光路差を式で示すことができるか
問３ 三角関数の計算をスムーズに行えたか
という点で、問１〜問３の全ての場所で差がついたと考えられます。
全体を通しての北海道大学の対策としては、
①典型問題をこなすことが基本。特別な対策は不要。
②素早く計算をするスキルも必要
③作図を積極的に行うマインドをもつ
というところがポイントだと思います。
学習、指導の参考になるでしょうか・・・他にもこんなところ気をつけたほうがいいよ！というのがあったら共有しましょう！
