教育改革がうたわれ、入試問題が大きく変化してきている時代です。
そこで、私が現在取り組んでいることを当ブログで紹介していこうと思います。
手始めに「概念理解問題」と称し生徒に課している問題から。
これらは思考力・判断力を身につけてもらうことが狙いです。
問題1 x-tグラフ
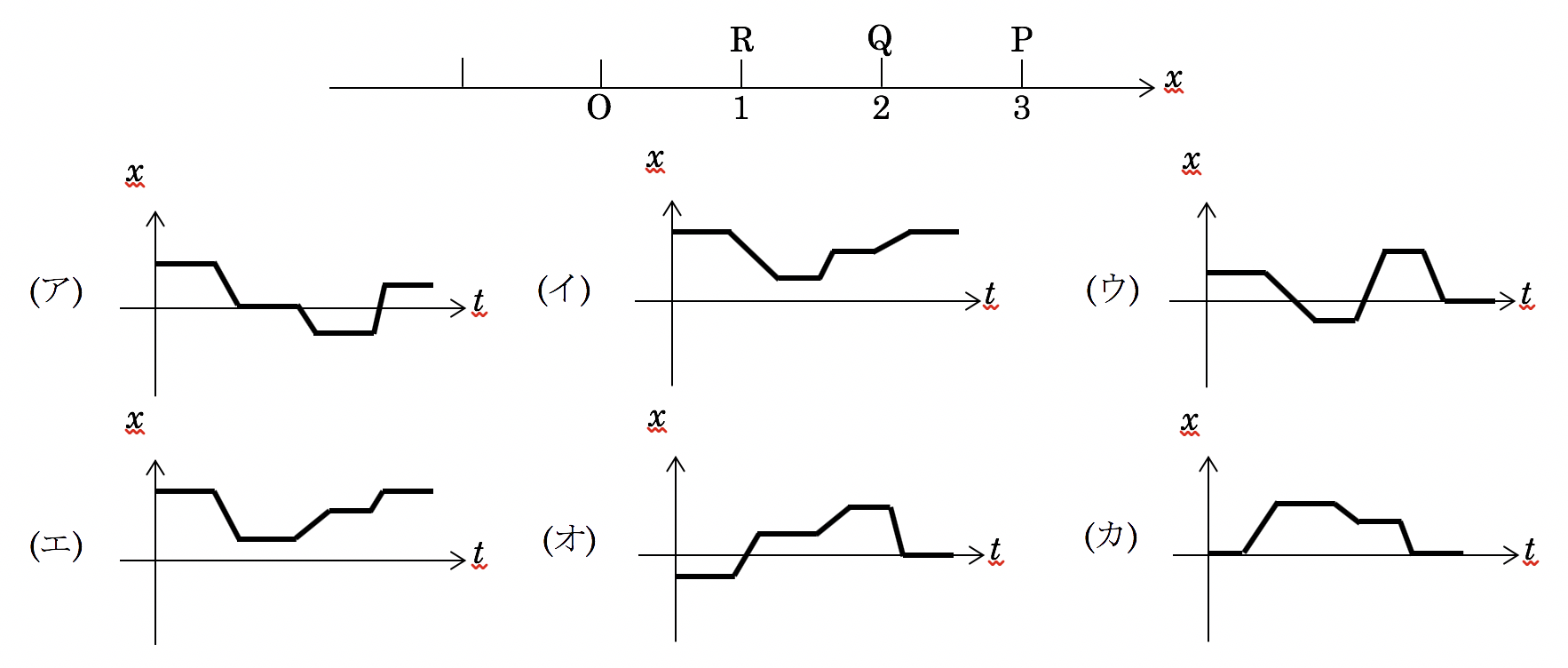
右向きを正としたx軸上に、下図のようにP点、Q点、R点、原点Oがある。P点で立ち止まっていた人がしばらくしてからR点に歩いて移動し、そこでしばらく止まっていた。その後、その人は走ってQ点に移動し少し休憩したあと、P点まで歩いて移動した。以下のグラフの中で、この人の動きを示すx-tグラフはどれか。画像の赤波線等はwordの校正マークです。無視してください。)
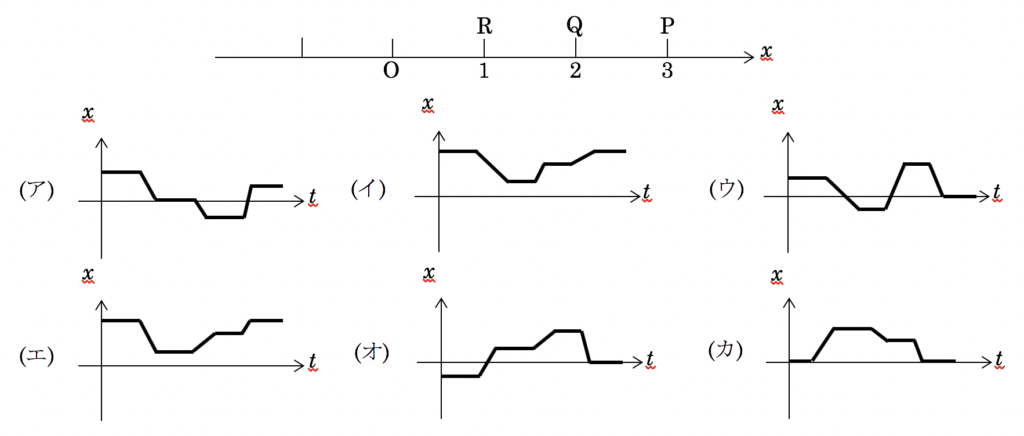
x-tグラフが一体何を示しているのかがわかっているかがポイントです。教員が時間をかけて伝えても、自分自身の頭で物体の動きをx-tグラフに投影していく練習を経ないと、生徒の理解はなかなか進みません。
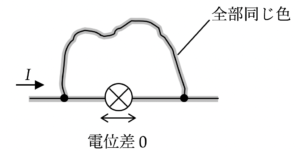
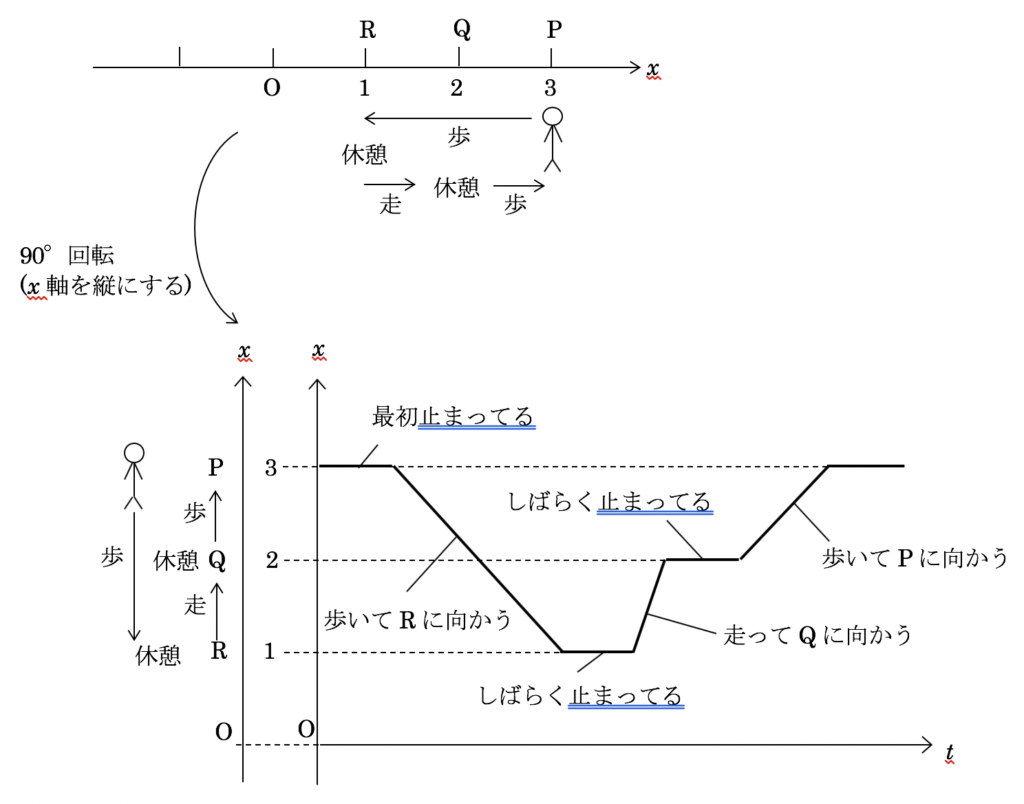
下図のように数直線を縦に回転させる発想を持たせることができたらスムーズに話が進みます。
x-t グラフが、物体の動きを示している、ということを理解した上で、最後に「走る」「歩く」の差で「傾き」の概念を伝えます。
問題2 曲線のx-tグラフ
ある電車が十分に長いまっすぐな線路を走っている。以下のグラフはある点を通過してからの列車の位置と時間の関係を示したものである。このグラフは列車がどのように運動していることを示しているか。
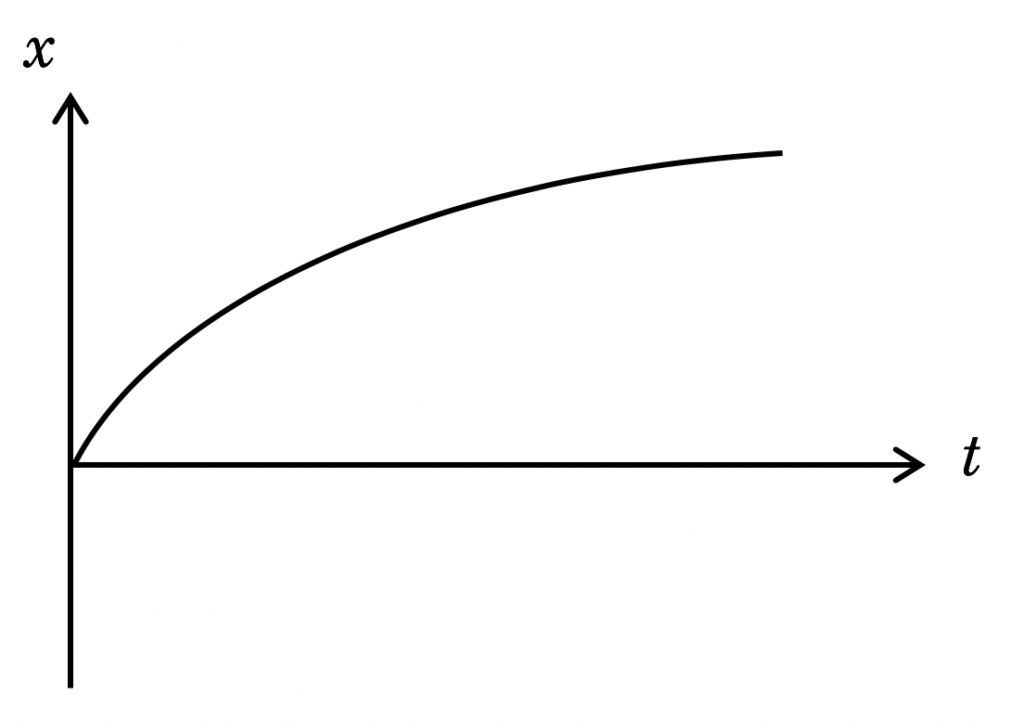
(ア) 常に速さが上がっている
(イ) 常に速さが下がっている
(ウ) 速さが上がっているときもあれば、下がっているときもある
(エ) 常に同じ速さで動いている
問題1でx-tグラフが何を示すかをなんとなく理解したところで、曲線のグラフをイメージすることに進みます。曲線が、だんだん速くなる物体を示していることは、習いたてでも十分理解が可能です。ここで「曲線の傾き」という概念にも触れます。
問題3 x-tグラフの傾き
以下は平行に並ぶ線路を走る2種類の電車A、Bの、位置と時刻を表したグラフである。選択肢の中で正しいことを述べているものを選べ。
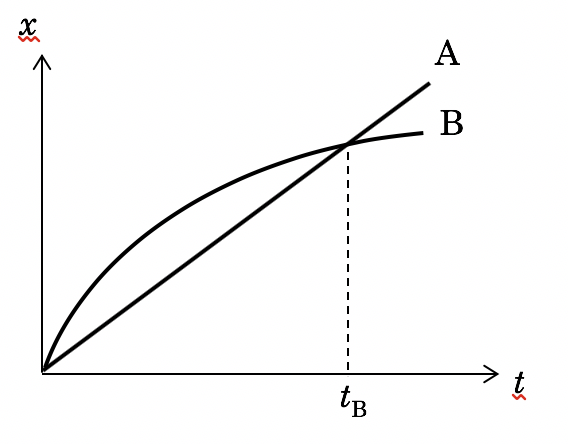
(ア) 時刻tBのとき、AとBは同じ速度である。
(イ) A、Bは常に速度を上げている。
(ウ) AとBが同じ速度になる瞬間が、tBよりも前にある。
(エ) グラフ内のどこかで、AとBの加速度が同じになるときがある。
生徒がx-tグラフにまだ慣れていないタイミングで扱うので、生徒に自由に解かせると、4つの選択肢を1つ1つを検討していく流れになります。その上で、グラフの交点という目立つ点が速度とは全く繋がりがないことに気づきます。ここで多くの生徒は驚きながら、グラフを理解します。
終わりに
私が授業でどのような問題を扱っているか、イメージだけでも伝わったでしょうか?決して簡単な問題ではないですが、生徒はよく頭を動かし取り組んでくれます。これが思考力・判断力の育成につながると私は考えています。
今後も色々な問題も紹介していきますのでお楽しみに。