Googleフォームで公開中の『スマホでできる小テスト』の解説ページです。一度解いてみてからの学習に活用してください。
今回は単振動の分野です。
受験用Googleフォームはこちら

・定義、概念を理解して
・典型問題をきちんとこなしたあと
取り組むことで力になる問題になっています。取り組むタイミングを間違えないようにしましょう。
問題1 単振動をする条件・復元力
単振動はどういった条件でおこるか.最適なものを1つ選べ.
ア. つりあいの点の周りならおこる
イ. つりあいの点から少しずれたときでも,つりあいの点に戻るような点の周りならおこる
ウ. フックの法則に従って力がはたらく点の周りでのみおこる
エ. どんな点でもおきる
解答 ウ
単振動は,復元力 $-mω^2x$がはたらくときにおこる.
復元力は,原点からの変位$x$に比例し,変位の向きと逆向きにはたらく力である.噛み砕いて説明すると,『中心からずれたとき,ずれればずれるほど大きな力で,中心に引き戻そうとする力』が復元力である.この力を説明しているのはイである.
ウのフックの法則に従って力がはたらく点でも単振動は起こるが,それ以外の力でも復元力となる場合もあるので,正解にはならない.
問題2 単振動の要素
図のような単振動をするとき,速度,加速度,物体にはたらく力の合力が,0,正に最大,負に最大となる点をそれぞれ選べ.ただし,右向きを正とする.
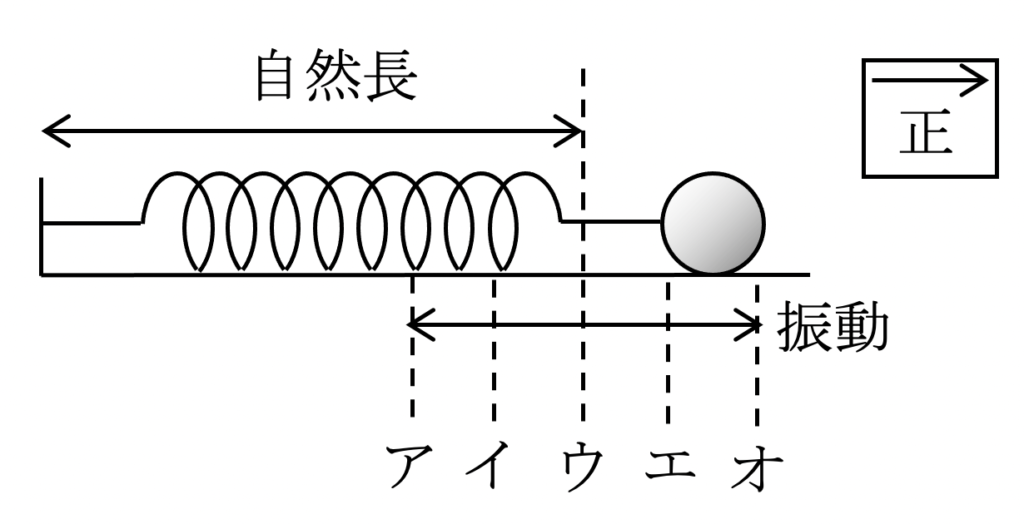
解答
| 0の点 | 正に最大の点 | 負に最大の点 | |
| 速度 | ア・オ | ウ | ウ |
| 加速度 | ウ | ア | オ |
| 合力 | ウ | ア | オ |
単振動は,単物体の往復運動(振動)の事であり,折り返し地点では,速度0,加速度最大.振動の中心では,速度最大,加速度0の運動を行っている.
『折り返し点』と『振動中心』がキーワードになるので頭に入れておこう.
また,加速度の原因は力であり,$ma=F$の関係で示されるので,加速度と力は同じ解答となる.
ばねが最も縮むときは,押し返す力が最も大きく(正に最大),ばねが最も伸びるときは,引き戻す力が最も大きい(負に最大)とばねの特徴からも答えられる.
問題3 単振動の周期
単振点Oを中心に点A,B間を周期6.0 sで単振動をしている物体がある.AからBに達するまでの時間と,BからOに達するまでの時間をそれぞれ求めよ.

ア. 5.0 s
イ. 4.0 s
ウ. 3.0 s
エ. 2.0 s
オ. 1.0 s
カ. 選択肢に適切な解答はない
解答
AからB:ウ
BからO:カ
単振動での時間に関する問題は,『距離÷時間』や,等加速度運動の式では求めることが できない.$\frac{T}{4}$ごとに対称性のある運動を行っているので,それを活用する.
(1)は$\frac{T}{2}$なので3.0 sでウ
(2)は$\frac{T}{4}$なので1.5 sでカ
となる.
問題4 単振動のエネルギー
なめらかな面上で一端を固定したばねにおもりをつける.おもりが静止していた座標$x’$ から,座標$x_0$までばねを伸ばして手を離したところ物体は単振動を行った.弾性力による位置エネルギー$U$と座標$x$の関係を示した$U−x$グラフを選べ.ただし,縦軸の0がグラフの原点とは限らないとする.
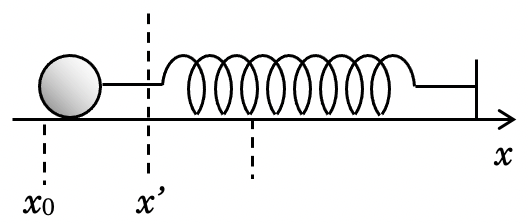
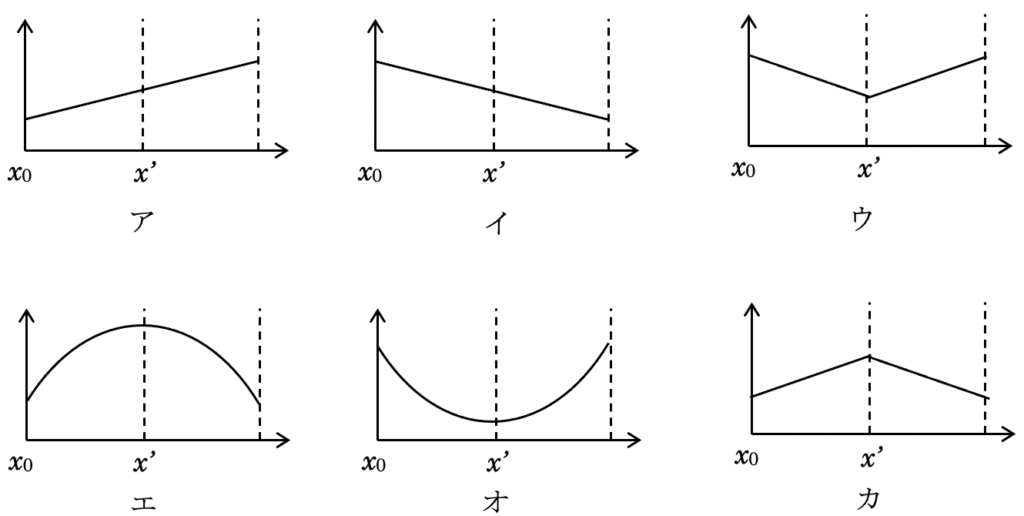
解答 オ
単振動ではいろいろな式が出てくるので,どれを使っていいかわからなくなることがあるが,きちんと『振動中心』や『折り返し点』のことを整理できれば,たいていのことはエネルギー保存則で十分計算できてしまう.エネルギーに関する考察をしてみよう.
最初に静止していた点$x’$は,力がつりあう点であり,そこは自然長であり,振動の中心となる位置となる.そこでは弾性力による位置エネは0となる.
そこから伸びや縮みがあると,$\frac{1}{2}kx^2$のエネルギーを持つので,エネルギーは振動の中心から離れるほど,2次的に増えていく.それを示したグラフはオ.
振動の中心で最も位置エネルギーが小さく,その分運動エネルギーが最大になっているというイメージを持っておこう.
問題5 単振動のエネルギー
前問と同じモデル において,運動エネルギー$K$と座標$x$の関係を示した$K−x$グラフを選べ.ただし,縦軸の0がグラフの原点とは限らないとする.


解答 オ
折り返し点で0,中心で最大,ということから,エか,カということはわかる.
しかし,運動エネルギーは$\frac{1}{2}mv^2$で示され,この式は$x$の関数ではないので,この公式からグラフを特定するのは難しい.そこで,力学的エネルギーの保存を手がかりに考える.
力学的エネルギーが保存することから,弾性力による位置エネルギーが減った分だけ運動エネルギーが増える,という関係から考えて,前問の解答であるオの変化に対応して変化しているようなグラフが正解になる.それを示したグラフはエ. ちなみに力学的エネルギーを示すグラフは横一直線で常に一定であるグラフになる.
振動の中心で最も位置エネルギーが小さく,その分運動エネルギーが最大になっているというイメージを持っておこう.

解説を読んだら再試験用のその2にぜひ挑戦してみてください.