2019年度北海道大学 前期 物理の問題を分析します。
私は夏休みに大学入試問題正解を使って、入試問題研究をしています。
予備校の先生は入試の終わる3月ごろから研究しているので、ざっと4ヶ月の遅れをとっていますが、そこは甘えてしまっています。解答を作ってくださっている先生方に感謝です。
せっかくブログを始めたので、入試問題研究も形に残していきたいと思います。
『大学入試問題正解 物理』は国立の北→南、私立の北→南という順番なので、最初は北海道大学からです。
1.問題構成
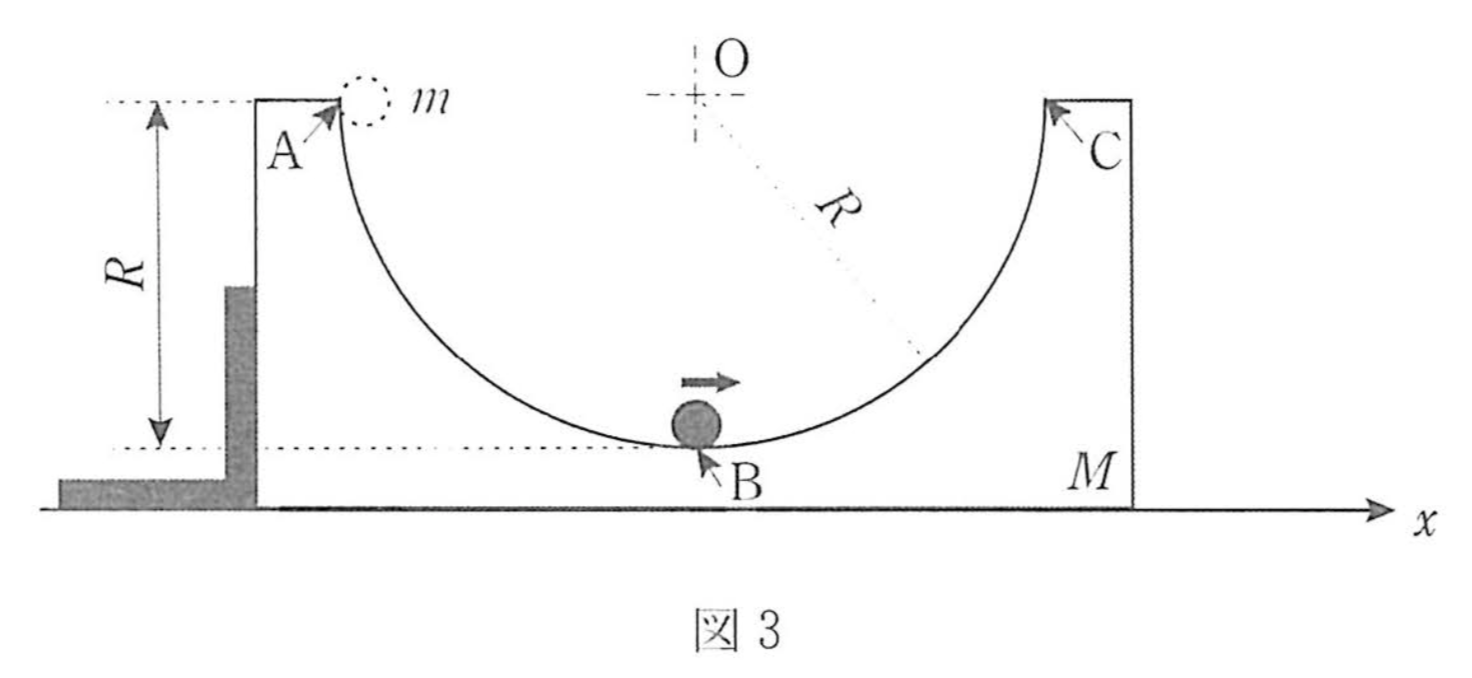
| 大問1 | 力学 | 動く半円形の台上での円運動 | 《定番 優しめ》 |
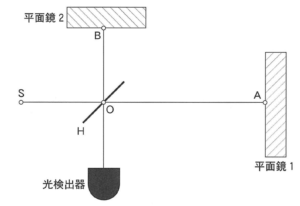
| 大問2 | 電磁気 | コンデンサー間の電場と、電荷が受ける力 | 《難しめ》 |
| 大問3 | 熱力学 | 球形容器内での気体分子運動論 | 《定番 優しめ》 |
問題のダウンロードはこちらから(リンク切れとなりました)
2.かかった時間
かかった時間:85分(試験時間は2科目で150分)
2科目同じ時間がかかったら解き終わらないですね。
計算自体は複雑にならないよう配慮されているので解きやすいです。
しかし問題量が多めです。
各大問の前半は基本的な問題で、後半は考えさせる問題や、計算量の多い問題になるので、前半を確実に取る練習が必要になります。
前半と後半の区切りが、ぱっと見ですぐわかるようになっているので、意識をするだけで、簡単に適切な時間配分を行えると思います。特別な技術は必要ありません。
3.筆者の正答率と各問題のポイント
| 大問1 | 完答 |
| 大問2 | (9)(10)で移項を間違える計算ミス(2問間違え) |
| 大問3 | (7)でミス、以降間違った答えを使用しているので(8)(9)(10)は× (11)は何しているのかわからなかった。(5問間違え) |
大問1について
前々年度あたりから急増している問題で、もはや定番となっています。
問3以降でひと工夫されていますが、保存則の成立条件から理解している受験生なら惑わされないはずです。

運動量 … 外力がはたらかない
左側にあるストッパーから外力が加わるので、物体が最下点に到達するまでの運動量は保存しない。最下点を通過したあとは、水平方向にはたらく外力がないので、水平方向の運動量は保存する。
エネルギー … 非保存力が仕事をしない
最下点に到達するまでは、垂直抗力が仕事をしないので、単純に成立。最下点以降は、垂直抗力が仕事をするので、球のみでは保存しない。球と台を合わせた系で考えれば、仕事は打ち消しあい保存する。
このような理解ができるように、生徒に仕込んでおきたいところです。
大問2について
電磁気の分野を苦手とする現役生がとても多いです。
実際に苦手としている生徒は、知っている解法や、公式に頼って解こうとしているように感じます。
そういった生徒にとって、この問題は難しく感じたのではないかと思われます。
極板間で及ぼしあう力を電場から考える問題自体は、受験生なら1回は解いたことがあるはず。しかし、「間に導体板を入れる」「導体板と誘電体の両方を使う」ということは未体験な生徒も多いと思います。
このとき、
電荷は保存されている→電気力線の本数も変わらない→電場が導体板を入れる前と変わらない。
誘電体を入れる→電場の式E=Q/εSの誘電率εの部分が変化する
この問題では、最初に電気容量Cが聞かれていますが、この点も生徒をこの発想から遠ざける一因になりそうです。Q=CVの公式に引っ張られてしまいます。
この点をうまく整理できたら、あとは典型問題ともいえるので、高得点を狙えるはずです。
前半が基本的、後半が難しめ、という全体の特徴の中で、前半につまづきポイントがあるという理由で、「難しめ」といえる大問です。
大問3について
球形容器の分子運動論の問題を解いたことがある生徒なら、問題なく前半はとけるはず。
後半については私の誤答を中心に紹介します。
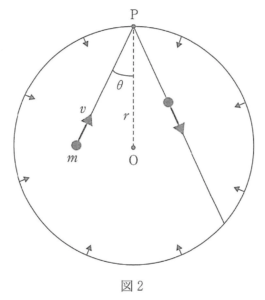
私は(7)「衝突後の速度」についての問いで、次のように立式して間違えました。

反射後の角度がθとはならないので、この立式は誤りになります。
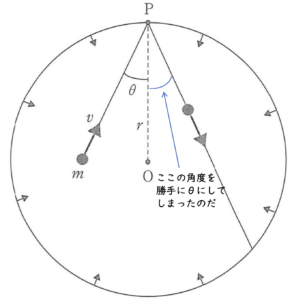 正しく立式すると、
正しく立式すると、

となります。
親切なことに問題文で、
「反射後のOP方向成分が(7)となる」
という穴埋めになっているので、このようなミスをしないように配慮がされているのに、これにも気づきませんでした。
(9)あたりを解いているときに、「cosθが消えそうで消えない、どこかで間違えたかな」と初めて違和感を持ちましたが、見直しても気づけない体たらく。悲しい。
その後の計算は簡単な誘導だったので、考え方の方針自体は間違えずに進めました。受験生もこの誘導に乗るのに苦労はないと思われます。
そして最後の問題(11)については、何を聞かれているのかさっぱりわからず、解説をみて、ここまで出てきた数式をなんとかいじくり回して答えに到達しました。
しかし結局何を解いているのかがわからず仕舞いです。
答えの
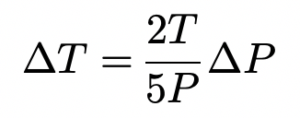
という式から読み解くと、
温度が高いときほど、圧力変化による温度変化が大きい。
圧力が高いときほど、圧力変化による温度変化が小さい。
という風に説明はできます。
そこからグラフを書いてみたりすると物理的な理解につながるかもしれないですが、この問題では式を出すところまでしか行なっていないので、それが出題者の意図なのかはわからないです。
はたして!!
4.次回は・・・
次回は北海道大学後期をやります。頑張ろう!