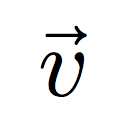
物理の教科書で速度が登場するときは、次のように書かれます。
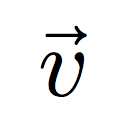
文字の上に矢印が書いてあります。これはベクトルであることを示す文字装飾です。しかし、この記号を授業で書くか書かないかは、物理教員の中でも別れていると思います。
ちなみに私は生徒にベクトル記号をしっかりと記入してもらいたと考えています。
さて、今回はこの表記の必要性について考察していきましょう。
(1.2はベクトルについての基本的な説明です。理解のある人は目次の3に飛んでください)
目次
1 ベクトルとは
ベクトルとは「向き」と「大きさ」を持つ量のことです。「東に3.0 m/s」や「北に4.0 m/s」という表現は向きと大きさを示しています。(「質量5.0 kg」などには向きがありません。これをスカラーといいます)
ベクトルを文章ではない方法で示すことができるのが作図です。
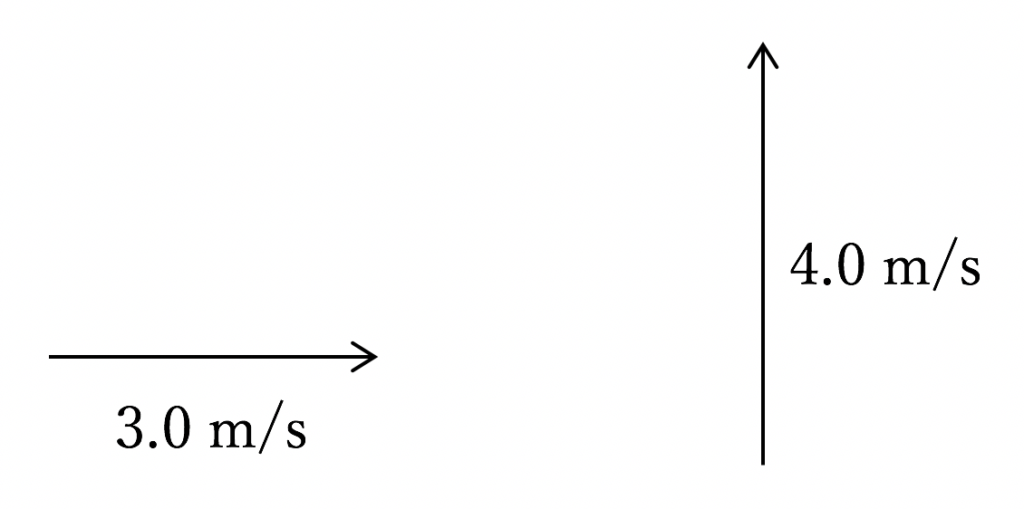
このように矢印を使うと「向き」は矢印の向きで、「大きさ」は矢印の長さ、で示すことができます。
2 ベクトルの計算の特殊さ
ベクトルの計算というのはある条件下で特殊になります。
例えば、直線上の速度の足し算を考えて見ます。エスカレーターの上でさらに歩いているようなイメージです。
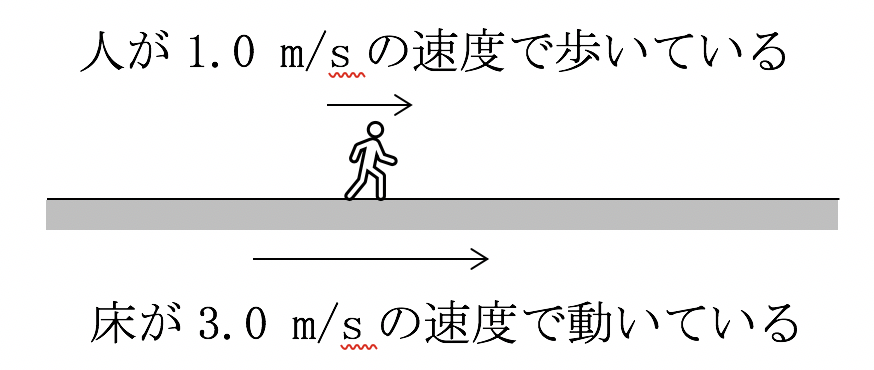
すると、人は4.0 m/sの速度で素早く移動できます。計算式にすると、
3.0 m/s + 1.0 m/s = 4.0 m/s
なんの変哲も無い足し算です。
しかしこれが、平面の場合(直線上ではない場合)、計算が特殊になります。例えば、船の上で歩くようなイメージをしてみます。
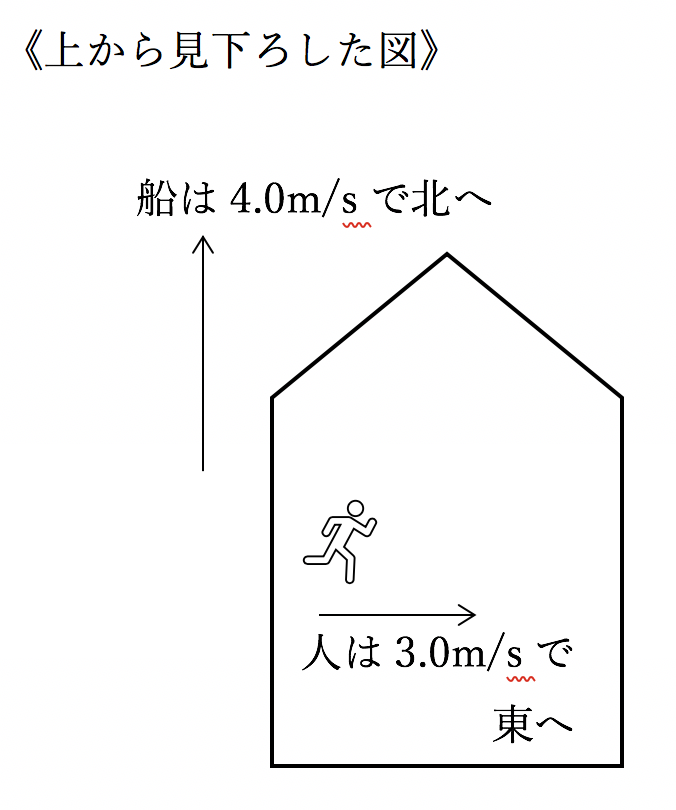
このような場合、人は北の速度と東の速度を合わせて、北東の方に進みます。そして、その大きさは、作図より5.0 m/sと計算します。
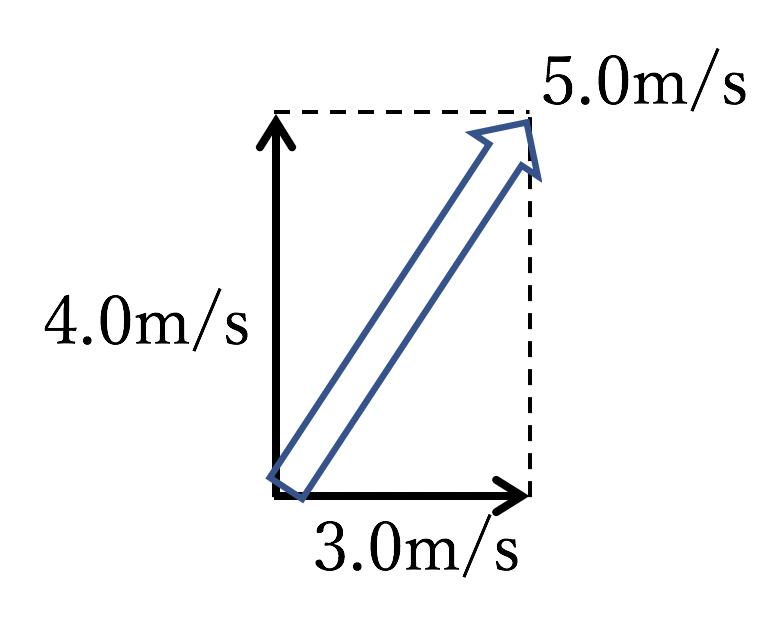
合わせた大きさは、4.0m/s + 3.0m/s=7.0 m/sとはならないのです。作図をし、矢印の長さを計算することで、大きさを求めるという計算になります。この例だと、3:4:5の有名三角形であることを利用できます。
3 ベクトル記号を生徒にしっかり書いてもらう意義は何か
ベクトル記号を書かせるのは、すごく形式的なことに見えて、物理の本質から外れていると考えてしまうかもしれません。
「記号をきちんと書くよりも、作図ができるようになって欲しいな」
「記号を書くことに注意を払うくらいなら、運動方程式を正しく立式できるようになって欲しいな」
このように考える先生も多いかと思います。
生徒が一度に注意をさける量には限りがあります。これをメモリと表現したとき、「記号をきちんと書かせる」ということにメモリを使ってしまうのはもったいない、という考え方です。決して間違った考え方とは思いません。
しかし、ベクトル記号を書かせることは、遠回りだけれど本質を理解する手助けになると私は考えます。また、独学で学ぶ生徒はこの部分を自分で不要と判断しがちなので、こちらから重要だと入念に伝える必要もあるでしょう。
具体的には、ベクトル記号を書くことで、「どの物理量がベクトルで、どの物理量がスカラーか」ということと、「ベクトル量を考えるときは、向きを区別する必要があるんだ」ということを自然と意識できるようになっていき、深い理解につながっていきます。
4 生徒がベクトル量をベクトル量と意識できることのメリット
4-1 直線上なら値の足し算でOK 平面だとダメ
初期のレベルだと足し算の方法を間違える生徒が減ります。
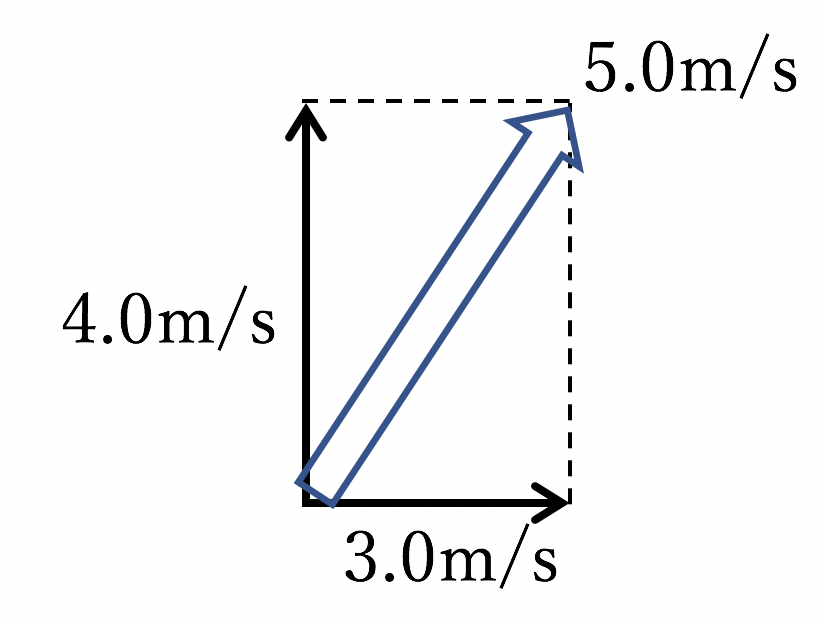
真上方向のベクトルと、真右方向のベクトル計算をするとき、何回伝えても、合成ベクトルを3.0 + 4.0 = 7.0 と計算してしまう生徒がいます。
最初の習得に非常に困難を伴いますが、下図のようにベクトルの書き方を示し、「ベクトルの足し算」を図でも式でも理解してもらうことで、計算方法の誤りというのは単純に起きづらくなります。時間をかければ、中3でも表記方法と計算方法を正しく習得することが可能です。
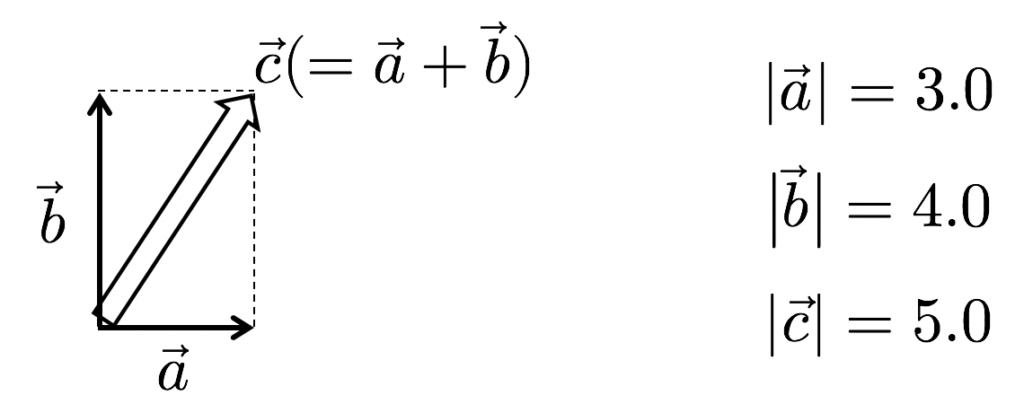
個人的な体感ですが、初めて平面での計算を学んでから次の単元くらいまでは、速度v、加速度a、力Fなどのベクトル量にはベクトル記号を必ずつけるのが良いと感じます。それ以降は生徒も理解を終えているので、特別に意識して欲しいとき以外は省略しても良いでしょう。
4-2 なぜベクトルを分解するのか理解できる
例えば、放物運動で初速度を分解するとき、2本の紐で物体をつるすとき、斜面上に物体を置いたときなどで、ベクトルの分解を行います。ここで生徒は「なぜ分解を行うのか」を意識していません。「分解する問題だから分解する」と勉強を進めてしまいます。
しかし、ベクトル記号を意識し、
「ベクトルの計算は直線上なら値を足し算できるけれど、平面だったら作図をして長さを求めていかないといけない」ということが体に馴染んできていけば、「分解をするのは、直線上に分けることで、値の足し算をするためだったんだ」ということが理解できます。
さらに
いままで分解して求めていたものを平面ベクトルとして考えてみよう、という本質的な問いにもつなげることができます。
これはとてもとても大切なことです。
さらにさらに
90度の関係にあるベクトルはそれぞれの方向に関与しない、という感覚を得ることにもつながります。
これもとてもとても大切なことです。
これらは、ベクトル量を重要だと意識していないと到達できない思考で、記号を丁寧にかき分けて行くことで意識する手助けになります。
5 分野別に活きる場面
4で紹介した通り、ベクトルをベクトルとして意識できると物理の本質的な学びに大きく役立ちます。この章では、分野別に特別に意識をしたい場面を紹介します。
5-1 円運動
等速円運動に関して、「等速」なのに「加速度」があることは、字面的にはおかしいともいえます。加速度があるなら変速するはずです。しかし、このときの「等速」はスカラー量である「速さ」が等しいことを示していて、ベクトル量である「速度」は、中心向きの「加速度」により「向きが変えられて」います。これはベクトルを強烈に意識させたい場面です。
5-2 運動量と運動エネルギーの正負に関して
運動量を習うとき、正負に関して無頓着になる生徒が多いです。しかし、運動量がベクトル量であることを意識すると、自然と正負を意識できる生徒もいます。
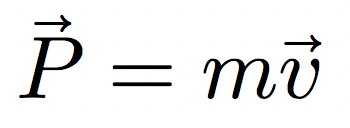
と表記し運動量もベクトル量であり、それは速度の向きと等しい、と理解し正負を正しく捉えたり、平面での運動量変化も思考できるように導きます。
また、運動エネルギーは2乗しているので向きがない量になっていることも合わせて伝えるのも良いでしょう。
5-3 磁束密度B
電磁誘導では、90度に交わるベクトルが登場し、フレミング左手につながります。向きがここまで習ってきたベクトルの関係性と大きく違うため、生徒にもある程度のレベルが必要ですが、うまく話すとレールや導体棒が斜めになった場合にも、鋭い視点を持って物理現象を考察できるような生徒に育つはずです。
6 終わりに
先生によって、意見が変わる内容かと思いますが、私が個人的に思っていることと、生徒の感じをまとめてみました。少しでも参考になればと思います。