生徒から頻繁に質問を受ける間違い例を紹介します。
1 静止摩擦力の大きさはμNではないの?
生徒は公式が好きです。だから公式R0=μNを習うと、静止摩擦力の計算で必ずこれを使おうとします。しかしこれは誤りです。
例えば以下のような図で考えてみましょう。

物体が動かない(静止したまま)であるなら、物体にはたらく力はつりあっています。なので、ここではたらく力はそれぞれ以下のようになります。
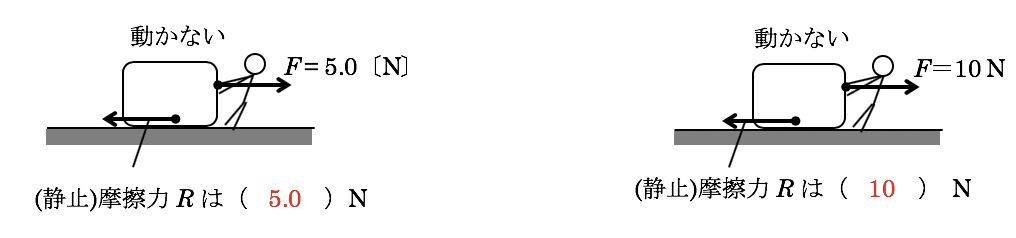
摩擦力をRと置いてつりあいの式を立てると、
左図 R=5.0N 右図 R=10N
と立式できて、Rを求めることができるんですね。
静止摩擦係数μは大きさを求めるのに使いませんでした。
外からの力が増えていき、すべり出してしまうようなギリギリの状態のときのみ、R0=μNが成り立ちます。
これは生徒が自ら気づくのは厳しいポイントなので、教員から丁寧に伝えてあげたほうが良いです。
2 こんな問題のときに間違いが起こる
実際に学び始めで基礎的な問題を解いているうちは、R0=μNという計算を行なう問題が多いので、生徒は間違いに気づきません。次のようなモデルを通して、考察をする機会をどこかで設けたいところです。

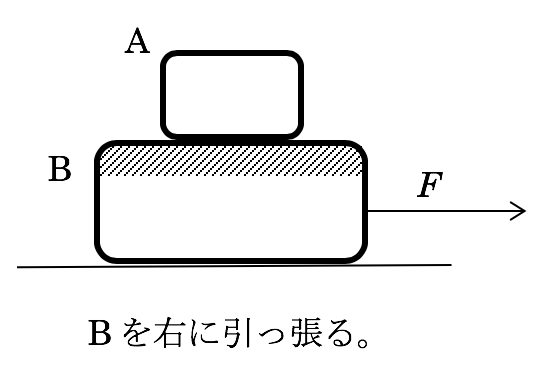
このように引っ張るとき、Fが小さいうちは、2物体は一体となり動きます。ここで生徒が間違えやすいポイントが実は2つあります。
一体となって動いたときに、はたらいている力は静止摩擦力!
動いているのに「静止」摩擦力なんです。動いているから動摩擦力、と考えてR’=μ’Nとしてしまう生徒が一定数います。
静止摩擦か動摩擦かは「動いているか」ではなく「すべっているか」で判断するんですね。
静止摩擦力の大きさはR=μNではない!
ここで今回のテーマになります。
静止摩擦の大きさはギリギリAがすべり出してしまうときのみμNが成り立ち、Fが小さいときはそうではありません。
十分にFが小さいときは、摩擦力をRと置き、物体それぞれで運動方程式を立てて解きます。
ただ解法を示すのではなく、間違えやすいポイントをきちんと伝えるようにして、この問題を扱いたいです。その上で次のようにまとめます。
①すべっているかどうか見極める
②すべっていなかったら摩擦をRと置き、つりあいや運動方程式を立式
③すべり出す瞬間であるなら、静止摩擦力の大きさはR=μNで出すこともできる
④すべっていたら動摩擦力がはたらく。動摩擦力は常にR'=μ’Nが成り立つので公式を利用する
3 番外編
他によくある間違いもついでに紹介します。
垂直抗力の大きさNはいつもN=mgではない!
生徒の多くはN=mgという公式があると思っています。しかしNの大きさは面と垂直方向のつりあい(または運動方程式)で求めます。上に引っ張る力があればその分Nは小さくなります。
例えば以下の問題で考えましょう。

Nとmgの大きさを比べたとき、
Fsinθ+N=mg
という式を立てることができれば、正しい関係がつかめて、いつもN=mgとはならないことを実感できます。
この問題は摩擦を学ぶ後半で触れさせたいです。
グループ討論をさせるにも最適な問題です。
4終わりに
以上、摩擦に関する生徒の間違えやすいポイントでした。釈迦に説法かと思いますが、授業に活かしていただければと思います。