日経サイエンス2013年1月号より、雑談ネタです。ヒッグス粒子という重力に関与する素粒子の発見が話題になった頃の記事です。高校で習う公式ですが、ただ覚えるだけになりがちな公式なので、こんな雑談をして膨らましてはどうでしょう。
1 万有引力の逆二乗則とは
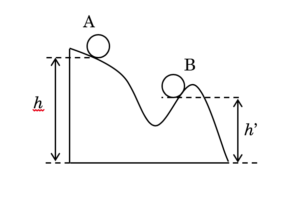
高校で習う万有引力の法則は2物体の距離をr、2物体の質量をm1、m2として以下のように示されます。
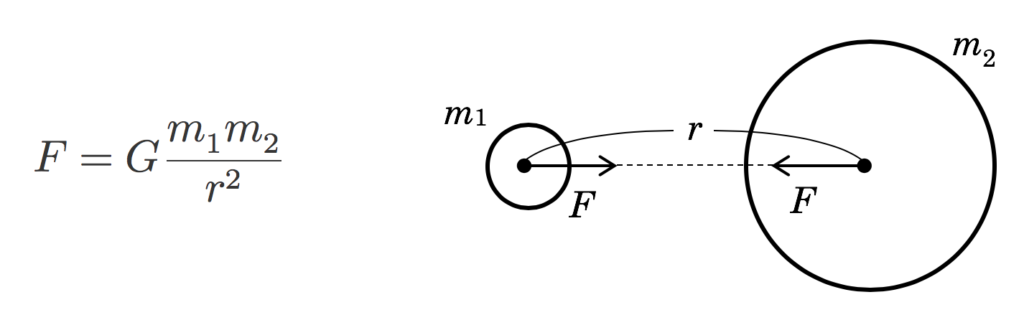
質量を持つ2物体はお互いにFの力で引き合います。これが万有引力の法則です。
公式の分母にr2があるので、距離が2倍になると力の大きさは4分の1に、距離が3倍になると力の大きさは9分の1になります。これを「重力の逆2乗則」と呼びます。
高校生には、「この公式は覚えるしかないよ、理屈はないよ」と学校では教えます。この式を導く理論はなく、理論値と実際値にズレがないことで、「この公式は正しい」としている式なのですね。
2 逆2乗則の確かめには月を使える
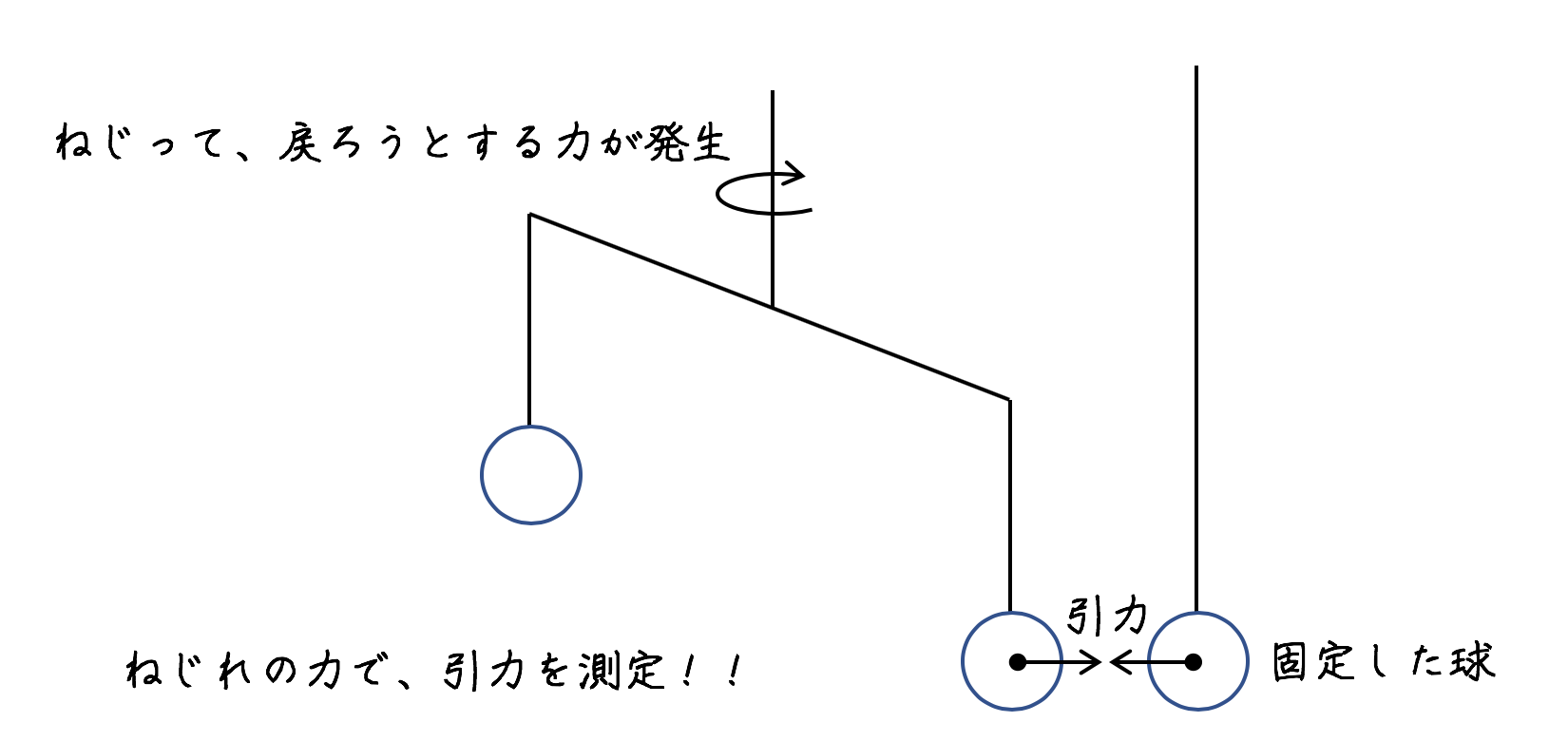
万有引力の法則発見当初は、紐をねじって、そのねじれが戻ろうとする力と、万有引力の大きさのつりあいから万有引力の法則を確かめることができていました。以下はその概略図です。ねじれ天秤といいます。

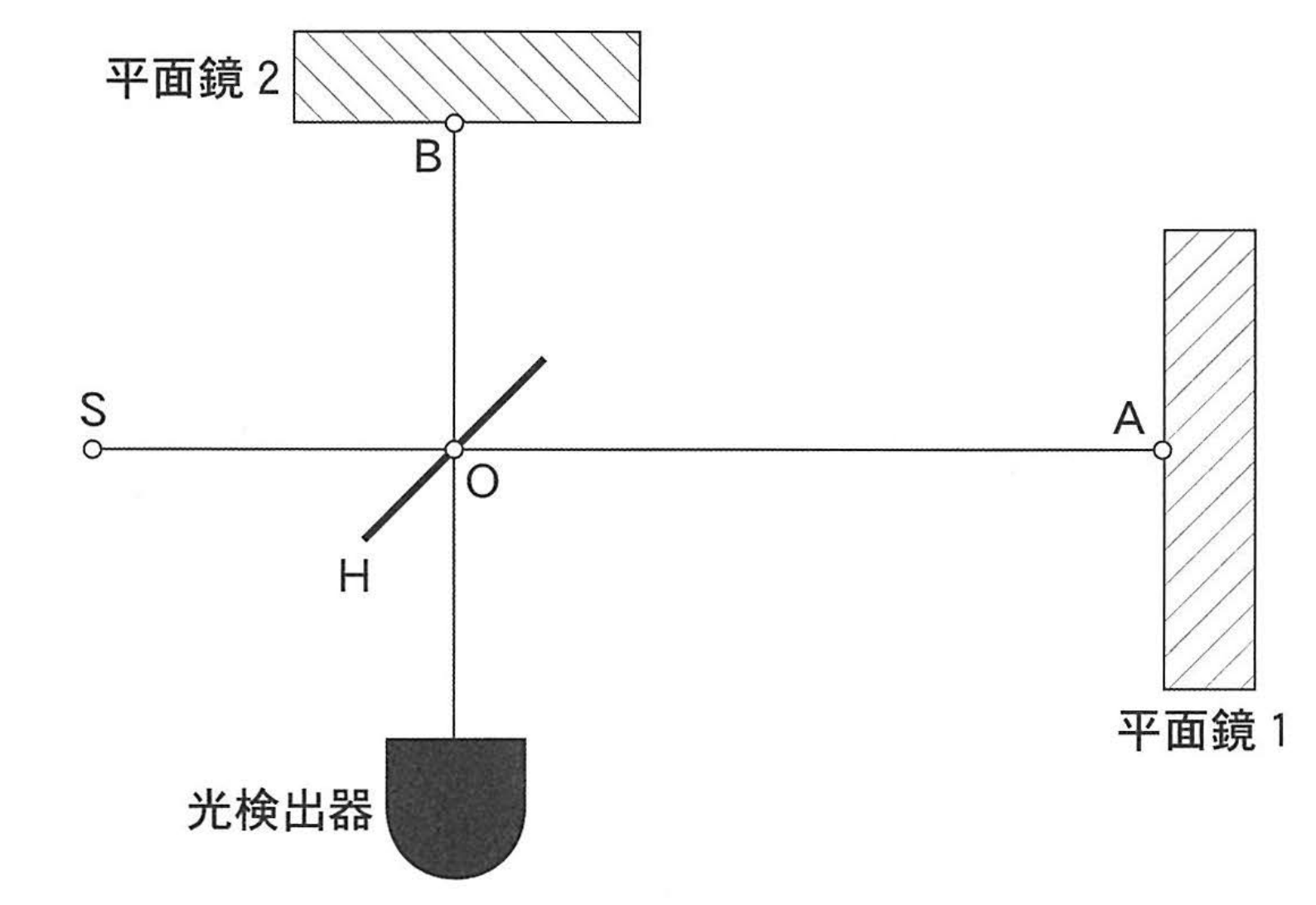
さて現代では、アポロ計画で月面に設置されたレーザー反射鏡を用いた計測でとても高精度な測定ができるようになりました。地球からレーザー光を照射、再び地球に戻ってくるまでの時間から月と地球間の距離が超精密に求まります。この距離測定を継続的に行い、自転軸の傾きの変化を求め、逆2乗則による理論値との比較を行うことで、逆2乗則が正しいことを確かめることができます。
月を使った測定はとても高精度な結果が出せます。地球上での実験では、空気抵抗や電気力が測定の邪魔をするので、それが影響しない月の測定はすごく制度の高いものになります。
3 遠距離はいい、しかし短距離は難しい
月を使って逆2乗則の正しさを測定していきましたが、逆に距離が短いときは電気力の影響など情報にノイズが入ってしまいます。そのノイズがとても大きいため、短距離での逆2乗則の測定はほったらかしにされてきました。
我々人類は数nmというとても小さい距離を操作したり、分析したりできる技術を持っているはずなのに、逆2乗則の測定は数mmという距離までしか確かめていなかったのです。数mmなんていうのは、目で判別できるほどの距離、最新技術から比べたらもう結構な距離です。

重力子やヒッグス粒子などの発見で重力関係の話題がホットになってきたところで、短距離の測定に注目が集まってきました。非常に短い距離のとき、逆2乗則が成り立たなくなるかも、という理論が出てきたからです。
4 力線による逆2乗則の説明と、余剰次元への拡大
重力の説明には、「重力場」という場学の理論を使ったりします。場学では力線を基本に力を考えます。力線は、密集しているほど大きく、スカスカなほど力が弱いとします。高校生も電磁気の分野で電気力線を習うのでこの話をしても通じるはずです。
そして、力線の密度を求めるために、球の表面積を使います。
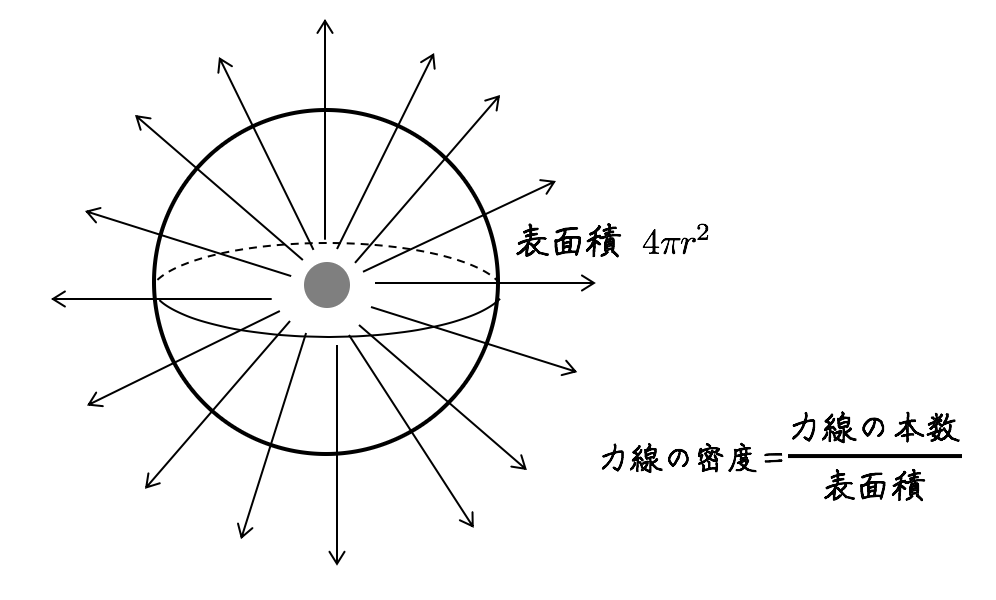
力線の密度を求めるときに、表面積(4πr2)で割るので、分母に距離の2乗が現れ、力の大きさが距離の逆2乗則になると考えられるのです。
そして現在、素粒子レベル、超ミクロの世界になると、重力子の振る舞いが4次元空間だったり、7次元空間だったりになるという理論が提唱されています。これを余剰次元の理論といいます。
そして、表面積の計算が4次元であるならrの3乗、7次元ならrの6乗という形に変化します。
表面積がこのように変化するので、万有引力の逆2乗則は4次元なら逆3乗則、 7次元なら逆 6乗則になるという予測がされています。
ここまでの話はあくまで仮説の積み重ねですが、実際に超ミクロで万有引力の測定を行い、逆6乗則になっていることが確認されれば、この仮説を証明できることになります。
しかし、実際にミクロでの万有引力の測定は現状の技術では不可能です。ただし、測定距離を短くしていけばmm単位でも逆2乗則が逆3乗則くらいまでには破れる可能性もあります。法則の破れが発見されただけでも余剰次元の理論の信憑性がぐっと上がります。

5 終わりに
ここまでの話を高校生に雑談でする場合、4次元や7次元の話を具体的に行うことは不可能かと思います(私もわかってないぞ!!)。ただし、表面積の計算方法が変わることは何となく納得はしてくれるので、この話をして楽しめる生徒はいます。
公式をただ覚えないとダメだよ、というのではなく、電気力線の計算の復習につなげたり、逆2乗則と表面積の関係を話題に出したりできると、とても有意義な時間になります。ぜひぜひ。
https://cryptocasinohk.com/