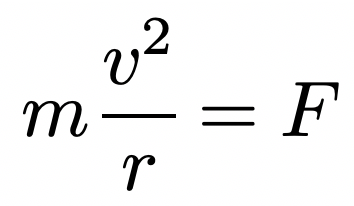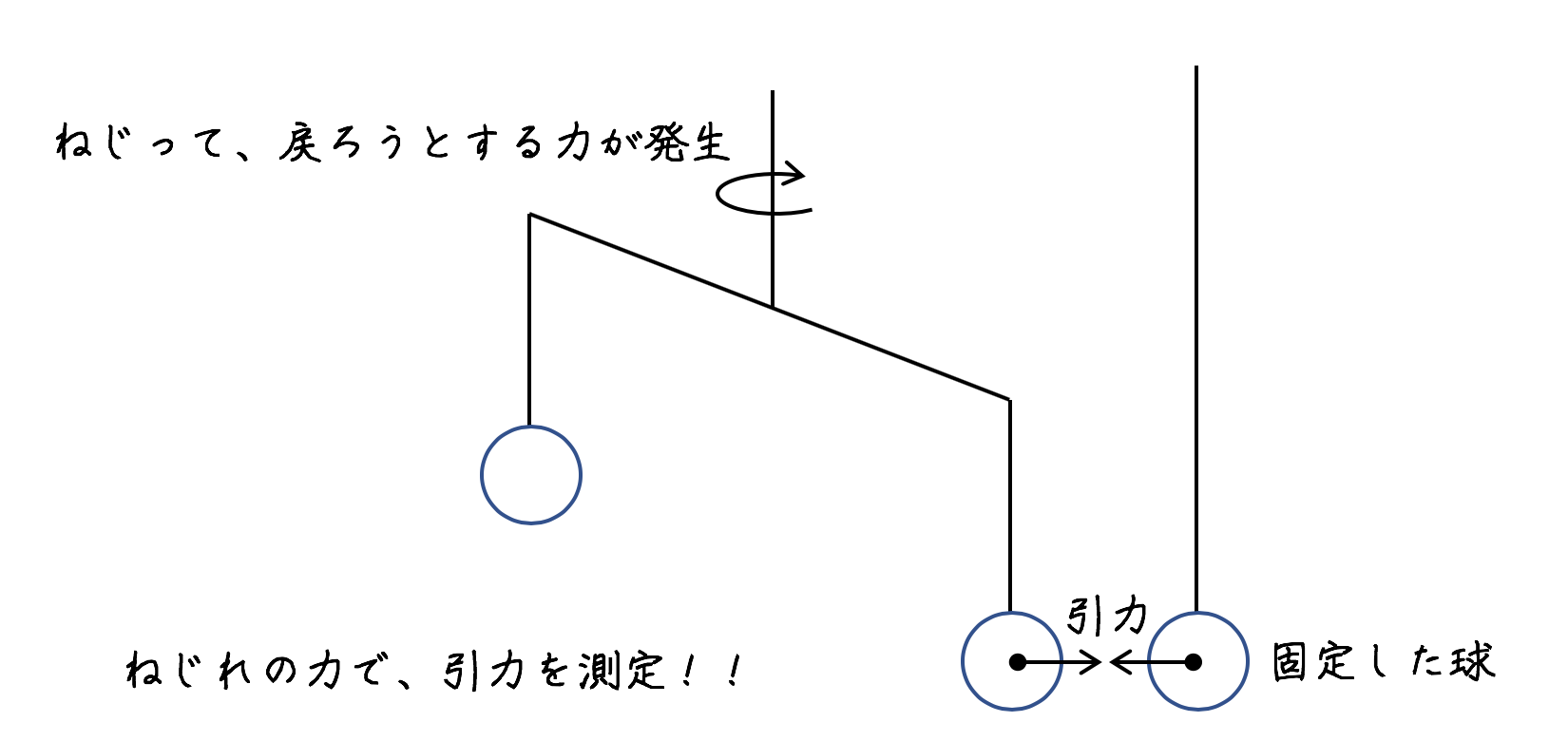
Googleフォームで公開中の『スマホでできる小テスト』の解説ページです。一度解いてみてからの学習に活用してください。
今回は運動量の分野です。
受験用Googleフォームはこちら

・定義、概念を理解して
・典型問題をきちんとこなしたあと
取り組むことで力になる問題になっています。取り組むタイミングを間違えないようにしましょう。
問題1 運動量と力積
質量がmと2mの2台のミニカーが、なめらかな床の上で静止している。2台のミニカーを同じ力で、同じ時間だけ押した。押した後のミニカーで運動量が大きいのはどちらか。
ア. 質量mの方
イ. 質量2mの方
ウ. どちらも同じ
解答 ウ
『運動量の変化量が力積』という関係がある。
今回、力Fで、同じ時間tだけ押されているので、力積の大きさはどちらも同じ。よって増加する運動量も同じである。
(運動量は同じだが、質量mがちがうので、速さvは異なる。軽い物体の方がより速くなる。)
問題2 仕事とエネルギー
質量がmと2mの2台のミニカーが、なめらかな床の上で静止している。2台のミニカーを同じ力で、同じ時間だけ押した。押した後のミニカーで運動エネルギーが大きいのはどちらか。
ア. 質量mの方
イ. 質量2mの方
ウ. どちらも同じ
解答 ア
運動量とエネルギーを混同しやすいので注意。『運動エネルギーの変化量は仕事』という関係から考える。
仕事は、『力F×距離x』、同じ時間だけ同じ力で押せば、軽い物体の方が長い距離を移動するので、される仕事は大きい。よって、軽い物体の方が押された後に持っている運動エネルギーは大きい。
運動方程式ma = Fから、軽いものの方が加速度aが大きくなり、同じ時間押した後の移動距離が大きいことを数式で示すこともできる。
また、運動エネルギーの公式で考えることは少し難しい。質量mの物体はmが小さいけれど、速度vが大きく、トータルでは質量2mの物体よりもエネルギーが大きいのだ。
問題3 力積の大小
ばねつき台車を壁に向かって走らせた衝突させたところ、図のような変化をした。車の運動量の変化が大きい順に>、=を用いて並び替えよ。ただし、右向きを正とし、値の大きさは、『正の値>0>負の値』とし、『-2 > -4』 という関係とする。
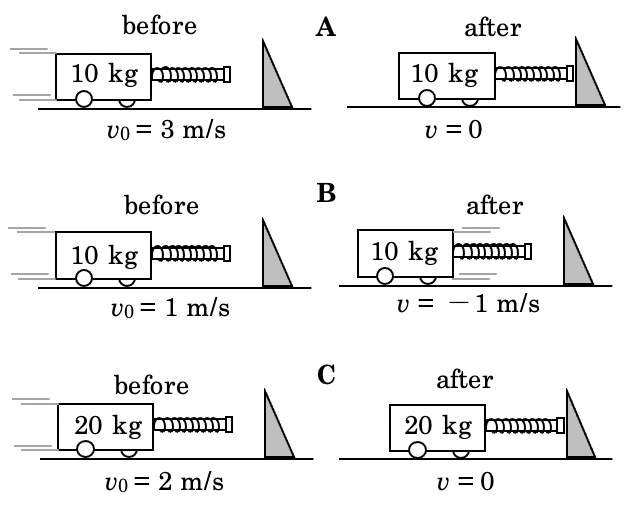
解答 B > A > C
変化といえば後-前、各問題で運動量の変化を計算する。その際、正負に気を付ける。
Aについて
衝突前の運動量 30 kg・m/s (質量×速度)
衝突後の運動量 0
⇒ 変化量 -30 kg・m/s
同様に求めると、
B:-20 kg・m/s
C:-40 kg・m/s
これらを大きい順に並び替えると、B > A > C
問題4 運動量保存が成り立つ条件
以下の中で、合計の運動量が保存している系をすべて選べ。
(ア) 雪上でスリップした車が、他の車に非弾性衝突した。2台の車を1つの系とする。雪上では摩擦はないとする。
(イ) ビリヤードで2つの弾が弾性衝突をした。2つのボールを1つの系とする。面はなめらかであるとする。
(ウ) ボールが地球に向かって落ちる。ボールを1つの系とする。
(エ) 静止したスケートボードにのりながら、地面をけって前に進んだ。人とスケートボードを1つの系とする。スケートボードと地面の間に摩擦はないとする。
(オ) 静止したスケートボードの上から、前に向かってジャンプした。人とスケートボードを1つの系とする。スケートボードと地面の間に摩擦はないとする。
解答 ア イ オ
運動量が保存する条件は、『はたらく力が内力のみであること』である。それで検証する。
(外力が働かないこととも言える。)
(ア) 〇 衝突時に、車同士で押しあう力がはたらき、それは内力となる。保存する。
(イ) 〇 はたらく力は球と球が押し合う力で、これは内力となる。保存する。
* 弾性衝突でも、非弾性衝突でも、運動量保存は成り立つ。
(ウ) × ボールにはたらく重力は、系の外の物体である地球から受ける力である。よって保存しない。保存則を成り立たせるには、ボールと地球を1つの系とすればよい。
(エ) × 地面をけった力の反作用で人は前に進む。この力は環境である地球から受ける力で、外力である。保存しない。
(オ) 〇 スケートボードの上からジャンプするときは、人とスケートボードの間で力を及ぼし合っている。これは内力である。保存する。
人が前に進んだ分、スケートボードは後ろに進む。
*(ウ) を除いて、物体に働く力として重力や垂直抗力を考察に入れていない。これらを考えると外力を受けていることになるので、保存則の成立条件を破るのだが、これは重力と垂直抗力がつりあっているので、プラマイ0になっているのだ。(ウ)に関しては、重力とつりあう力がないので無視できない。
また、これらは運動方向と90°の関係にあるので、運動に関与していない、と考えてもよい。水平方向の運動量が保存している。という考え方である。
問題5 運動量の保存
図のように、摩擦のないタイヤと斜面と壁のついた台車を静止させ、小球を自由落下させたところ、小球が点線のような軌道を通り、最終的に台車の左側へ飛んで行った。最終的に台車はどちらに動いているか。ただし、図の軌道は、台車上の観測者から見た軌道であり、台車が動かなかったことを示しているわけではないので注意せよ。
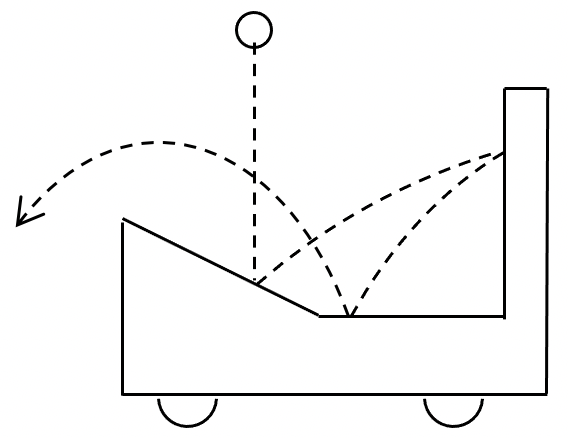
ア. 台車は右側に動いている
イ. 台車は左側に動いている
ウ. 台車は動いていない
エ. 情報が足りず答えられない
解答 ア
運動量保存則で考える。ボールを投げる前は、台もボールも静止している。よって運動量の和は0である。
そして、ボールが跳ね返った後は、ボールは左向きに運動量を持っている。
運動量保存則より跳ね返った後も運動量の和は0になるはずなので、台車は右向きの運動量を持っているとわかる。よってア。
問題6 運動量の保存
1本の木製のボーリングのピンにボールを転がして倒す。ボールは2種類あり、ひとつはゴムでできたボール、もうひとつは粘土でできたボールである。2つボールの大きさと質量は同じである。ボールをピンにぶつけると、ゴムのボールはね返ってきたが、粘土のボールはピンと一体になった。どちらのボールがピンを倒しやすいか。
ア. ゴムのボール
イ. 粘土のボール
ウ. 変わらない
エ. 情報が足りない
解答 ア
ゴムのボールは跳ね返ってきているということから、衝突前後の運動量変化はパテのボールより、ゴムボールの方が大きいといえる。ボールが受ける力積が大きいということは、ボールがピンに与える力積も大きいということになる。よって、ゴムボールの方が、ピンに与える力積が大きいためピンを倒しやすい。

またの閲覧をお待ちしています。
解説を読んだら再試験用の「その2」もどうぞ。